题目内容
已知抛物线y=x2-2px+16的顶点在坐标轴上,试确定p的值.
考点:二次函数的性质
专题:计算题
分析:先把抛物线解析式配成顶点式得到抛物线的顶点坐标为(p,16-p2),再根据x轴上点的坐标特征得到16-p2=0,然后解方程即可.
解答:解:y=x2-2px+16
=(x-p)2+16-p2,
所以抛物线的顶点坐标为(p,16-p2),
而顶点在坐标轴上,
所以16-p2=0,
解得p=4或-4.
=(x-p)2+16-p2,
所以抛物线的顶点坐标为(p,16-p2),
而顶点在坐标轴上,
所以16-p2=0,
解得p=4或-4.
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值
,即顶点是抛物线的最低点.
当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
时,y随x的增大而增大;x>-
时,y随x的增大而减小;x=-
时,y取得最大值
,即顶点是抛物线的最高点.也考查了二次函数图象与一次函数图象的交点问题.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,同心圆O,大圆的面积被小圆所平分,若大圆的弦AB,CD分别切小圆于E、F点,当大圆半径为R时,且AB∥CD,求阴影部分面积.
如图,同心圆O,大圆的面积被小圆所平分,若大圆的弦AB,CD分别切小圆于E、F点,当大圆半径为R时,且AB∥CD,求阴影部分面积. 如图为二次函数y=ax2+bx+c的图象,在下列说法中:
如图为二次函数y=ax2+bx+c的图象,在下列说法中: 函数y=x2+bx+c与y=x的图象如图所示,有以上结论:
函数y=x2+bx+c与y=x的图象如图所示,有以上结论: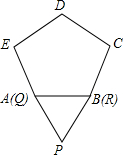 如图,将边长为1的等边△PQR沿着边长为1的正五边形ABCDE外部的边连续滚动(点Q、点R分别与点A、点B重合),当△PQR第一次回到原来的起始位置时(顶点位置与原来相同),点P所经过的路线长为
如图,将边长为1的等边△PQR沿着边长为1的正五边形ABCDE外部的边连续滚动(点Q、点R分别与点A、点B重合),当△PQR第一次回到原来的起始位置时(顶点位置与原来相同),点P所经过的路线长为 如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.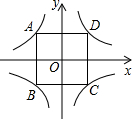 在同一平面直角坐标系中,反比例函数y=
在同一平面直角坐标系中,反比例函数y=