题目内容
在等腰梯形ABCD中,AB∥DC,CG⊥AB于点G,对角线AC⊥BD交于点O,EF是中位线.求证:CG=EF.
考点:等腰梯形的性质,梯形中位线定理
专题:
分析:作CH∥BD,交AB的延长线于H,得出四边形BDCH是平行四边形,同时得出∠ACH=∠AOB=90°,根据等腰梯形的性质得出AC=DB,从而证得AC=CH,证得△ACH是等腰直角三角形,根据等腰三角形的性质即可证得CG=
AH=
(AB+BH)=
(AB+DC),根据梯形的中位线定理得出EF=
(AB+DC),从而证得CG=EF.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: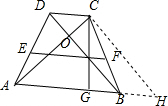 证明:如图,作CH∥BD,交AB的延长线于H,
证明:如图,作CH∥BD,交AB的延长线于H,
∴∠ACH=∠AOB,
∵AC⊥BD,
∴∠ACH=90°,
∵AB∥DC,
∴四边形BDCH是平行四边形,
∴DC=BH,BD=CH,
∵四边形ABCD是等腰梯形,
∴AC=BD,
∴AC=CH,
∴△ACH是等腰直角三角形,
∵CG⊥AB,
∴CG是等腰直角三角形ACH斜边的中点,
∴CG=
AH=
(AB+BH)=
(AB+DC),
∵EF是中位线.
∴EF=
(AB+DC),
∴CG=EF.
 证明:如图,作CH∥BD,交AB的延长线于H,
证明:如图,作CH∥BD,交AB的延长线于H,∴∠ACH=∠AOB,
∵AC⊥BD,
∴∠ACH=90°,
∵AB∥DC,
∴四边形BDCH是平行四边形,
∴DC=BH,BD=CH,
∵四边形ABCD是等腰梯形,
∴AC=BD,
∴AC=CH,
∴△ACH是等腰直角三角形,
∵CG⊥AB,
∴CG是等腰直角三角形ACH斜边的中点,
∴CG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵EF是中位线.
∴EF=
| 1 |
| 2 |
∴CG=EF.
点评:本题考查了等腰梯形的性质,平行四边形的判定和性质,等腰直角三角形的判定和性质,梯形的中位线定理等,作出辅助线构建平行四边形是本题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
某运动员为了备战2014年南京青奥会,刻苦进行训练,为了判断他的成绩是否稳定,教练对他近阶段10次训练的成绩进行统计和分析,那么教练最需要了解该运动员这10次成绩的( )
| A、众数 | B、方差 |
| C、平均数 | D、中位数 |
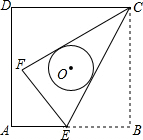 如图,正方形ABCD的边长为8,点E是AB边上的一点,将△BCE沿着CE折叠至△FCE,若CF、CE恰好与正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为( )
如图,正方形ABCD的边长为8,点E是AB边上的一点,将△BCE沿着CE折叠至△FCE,若CF、CE恰好与正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为( )| A、10 | ||||
B、8
| ||||
C、
| ||||
| D、以上都不对 |
 已知,△ABC内接于⊙O,AB=BC,∠BAC平分线交于⊙O于点P,自P点作PD⊥AB,垂足为D,求证:AB-AC=2BD.
已知,△ABC内接于⊙O,AB=BC,∠BAC平分线交于⊙O于点P,自P点作PD⊥AB,垂足为D,求证:AB-AC=2BD. 如图,同心圆O,大圆的面积被小圆所平分,若大圆的弦AB,CD分别切小圆于E、F点,当大圆半径为R时,且AB∥CD,求阴影部分面积.
如图,同心圆O,大圆的面积被小圆所平分,若大圆的弦AB,CD分别切小圆于E、F点,当大圆半径为R时,且AB∥CD,求阴影部分面积.