题目内容
15.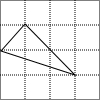 某同学在方格纸上画了四个三角形,与书本上的三角形(如图)相似的是( )
某同学在方格纸上画了四个三角形,与书本上的三角形(如图)相似的是( )| A. |  | B. | 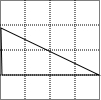 | C. | 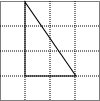 | D. | 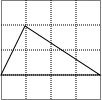 |
分析 先根据勾股定理得出题中给出的三角形的边长,再求出各选项中三角形的边长,根据相似三角形的判定定理即可得出结论.
解答 解:图中三角形三边长分别为:$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,$\sqrt{{2}^{2}+{2}^{2}}$=$\sqrt{8}$.
A、图中三角形三边长分别为2,$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,$\sqrt{{3}^{2}+{3}^{2}}$=$\sqrt{18}$与原三角形的三边不成比例,故本选项错误;
B、图中三角形三边长分别为2,4,$\sqrt{{4}^{2}+{2}^{2}}$=$\sqrt{20}$,
∵$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{8}}{4}$=$\frac{\sqrt{10}}{\sqrt{20}}$与原三角形的三边成比例,∴与书本上的三角形(如图)相似,故本选项正确;
C、图中三角形三边长分别为2,3,$\sqrt{{2}^{2}+{2}^{2}}$=$\sqrt{8}$与原三角形的三边不成比例,故本选项错误
D、图中三角形三边长分别为$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,4与原三角形的三边不成比例,故本选项错误.
故选B.
点评 本题考查的是相似三角形的判定定理,熟知三组对应边的比相等的两个三角形相似是解答此题的关键.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
20.如图,用火柴棒搭图形,第1个图形用了三根火柴棒搭出了一个等边三角形,第二个图形在第一个图形的基础上搭了一个每边是一根火柴棒的平行四边形,平行四边形与三角形的公共边只用一根火柴棒,依次交替搭下去搭出以后各个图形,记第n个图形用了an根火柴棒.

(1)填表:
(2)当n为奇数时,小明说:an=5n+3,小亮说:an=$\frac{5n+1}{2}$.你认为他们谁说得对?
并求当n为偶数时的an(用含n的代数式表示).
(3)an是否可取下列各值:2016,2015?若可取,求出此时n的值.

(1)填表:
| n | an | n | an |
| 1 | 3 | 2 | 6 |
| 3 | 8 | 4 | 11 |
| 5 | 13 | 6 | 16 |
并求当n为偶数时的an(用含n的代数式表示).
(3)an是否可取下列各值:2016,2015?若可取,求出此时n的值.
7.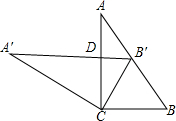 如图,将两块大小相同的三角板重叠在一起,∠A=30°,∠B=60°,BC=10cm,把上面一块三角板绕顶点C作逆时针方向旋转到△A′B′C′的位置,点B′在AB上,A′B′与AC相交于点D,则A′D的长度为( )
如图,将两块大小相同的三角板重叠在一起,∠A=30°,∠B=60°,BC=10cm,把上面一块三角板绕顶点C作逆时针方向旋转到△A′B′C′的位置,点B′在AB上,A′B′与AC相交于点D,则A′D的长度为( )
 如图,将两块大小相同的三角板重叠在一起,∠A=30°,∠B=60°,BC=10cm,把上面一块三角板绕顶点C作逆时针方向旋转到△A′B′C′的位置,点B′在AB上,A′B′与AC相交于点D,则A′D的长度为( )
如图,将两块大小相同的三角板重叠在一起,∠A=30°,∠B=60°,BC=10cm,把上面一块三角板绕顶点C作逆时针方向旋转到△A′B′C′的位置,点B′在AB上,A′B′与AC相交于点D,则A′D的长度为( )| A. | 14cm | B. | 15cm | C. | 16cm | D. | 17cm |
5.若k为任意实数,则抛物线y=-2(x-k)2+k的顶点在( )
| A. | 直线y=x上 | B. | 直线y=-x上 | C. | x轴上 | D. | y轴上 |
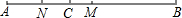
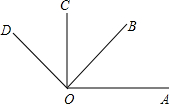 已知∠AOC,∠BOD都是直角,∠BOC=50°
已知∠AOC,∠BOD都是直角,∠BOC=50° 图中线段AB表示某工程的部分隧道,无人勘测飞机从隧道的一侧点A出发,沿着坡度为1:1.5的路线AE飞行,飞行至分界点C的正上方点D时,测得隧道另一侧点B的俯角为23°,继续飞行至点E,测得点B的俯角为45°,此时点E离地面的高度EF=800米.
图中线段AB表示某工程的部分隧道,无人勘测飞机从隧道的一侧点A出发,沿着坡度为1:1.5的路线AE飞行,飞行至分界点C的正上方点D时,测得隧道另一侧点B的俯角为23°,继续飞行至点E,测得点B的俯角为45°,此时点E离地面的高度EF=800米.