题目内容
5.如图,线段AB=10cm,C是线段AB上一点,BC=6cm,M是AB的中点,N是AC的中点.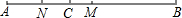
(1)图中共有10条线段;
(2)求线段AN的长;
(3)求线段MN的长.
分析 (1)根据线段有两个端点,写出所有线段后计算个数;
(2)由N是AC中点知AN=$\frac{1}{2}$AC,而AC=AB-BC,根据AB、BC的长度可得;
(3)由图可知,MN=AM-AN,由M是AB中点且AB=10cm可得AM长度,由(2)知AN的长度,可得MN长.
解答 解:(1)图中的线段有AN、AC、AM、AB、NC、NM、NB、CM、CB、MB这10条;
(2)∵AB=10cm,BC=6cm,
∴AC=AB-BC=4cm,
又∵N是AC的中点,
∴AN=$\frac{1}{2}$AC=2cm;
(3)∵AB=10cm,M是AB的中点,
∴AM=$\frac{1}{2}$AB=5cm,
由(1)知,AN=2cm,
∴MN=AM-AN=3cm;
故答案为:(1)10.
点评 本题考查了两点间的距离:连接两点间的线段的长度叫两点间的距离.距离是一个量,有大小,区别于线段,线段是图形.线段的长度才是两点的距离.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
15.声音在空气中传播的速度y(米/秒)(简称音速)与气温x(℃)的关系如下表:
①观察上表,气温每升高5℃,音速如何变化?
②求出y与x之间的表达式;
③气温x=22℃时,某人看到烟花燃放5秒后才听到响声,那么此人与烟花燃放处的距离多远?
| 气温x(℃) | 0 | 5 | 10 | 15 | 20 |
| 音速y(米/秒) | 331 | 334 | 337 | 340 | 343 |
②求出y与x之间的表达式;
③气温x=22℃时,某人看到烟花燃放5秒后才听到响声,那么此人与烟花燃放处的距离多远?
16. 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法不正确的是( )
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法不正确的是( )
 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法不正确的是( )
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法不正确的是( )| A. | AD是∠BAC的平分线 | B. | ∠ADC=60° | ||
| C. | 点D是AB的垂直平分线上 | D. | 如果CD=2,AB=7,则可得S△ABD=14 |
10.下列分解因式结果正确的是( )
| A. | y3-y=y(y2-1) | B. | x2-x-3=x(x-1)-3 | C. | -m2+n2=-(m-n)(m+n) | D. | x2-3x+9=(x-3)2 |
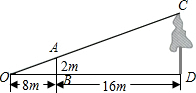 如图,为了测量校园内某棵树的高度,张敏用长为2m的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点O处.此时,竹竿与O点相距8m,竹竿与树相距16m,则树的高度为6m.
如图,为了测量校园内某棵树的高度,张敏用长为2m的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点O处.此时,竹竿与O点相距8m,竹竿与树相距16m,则树的高度为6m.
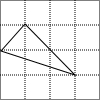 某同学在方格纸上画了四个三角形,与书本上的三角形(如图)相似的是( )
某同学在方格纸上画了四个三角形,与书本上的三角形(如图)相似的是( )