题目内容
20.如图,用火柴棒搭图形,第1个图形用了三根火柴棒搭出了一个等边三角形,第二个图形在第一个图形的基础上搭了一个每边是一根火柴棒的平行四边形,平行四边形与三角形的公共边只用一根火柴棒,依次交替搭下去搭出以后各个图形,记第n个图形用了an根火柴棒.
(1)填表:
| n | an | n | an |
| 1 | 3 | 2 | 6 |
| 3 | 8 | 4 | 11 |
| 5 | 13 | 6 | 16 |
并求当n为偶数时的an(用含n的代数式表示).
(3)an是否可取下列各值:2016,2015?若可取,求出此时n的值.
分析 (1)根据图形的变化,可知偶数下标比前一个图形多3根,奇数下标比前一个图形多2根,套入数据即可得出结论;
(2)根据图形的变化,可知偶数下标比前一个图形多3根,奇数下标比前一个图形多2根,将n分奇偶处理,看1到n中有多少个偶数和奇数,从而得出结论;
(3)令an=2016,an=2015,套用(2)得出的结果即可结论.
解答 解:根据图形的变化,可知图2比图1多3根火柴棒,图3比图2多2根火材棒,图4比图3多3根火柴棒…,即多的数目3、2交替.
(1)a3=a2+2=6+2=8,a4=a3+3=8+3=11,a5=a4+2=11+2=13,a6=a5+3=13+3=16.
故答案为:8;11;13;16.
(2)a1=3=1+2.
当n为奇数时,1到n中有$\frac{n-1}{2}$个偶数,有$\frac{n+1}{2}$个奇数,
结合发现的规律可知:an=1+$\frac{n+1}{2}$×2+$\frac{n-1}{2}$×3=$\frac{5n+1}{2}$,
故小亮说的正确.
当n为偶数时,1到n中有$\frac{n}{2}$个偶数,有$\frac{n}{2}$个奇数,
结合发现的规律可知:an=1+$\frac{n}{2}$×2+$\frac{n}{2}$×3=$\frac{5n+2}{2}$.
(3)令an=2016,即$\frac{5n+1}{2}$=2016,或$\frac{5n+2}{2}$=2016,
解得:n=$\frac{4031}{5}$,或n=806;
令an=2015,即$\frac{5n+1}{2}$=2015,或$\frac{5n+2}{2}$=2015,
解得:n=$\frac{4029}{5}$,或n=$\frac{4028}{5}$.
综上可知,an能取2016,此时n的值为806.
点评 本题考查了图形的变化,解题的关键是:发现“偶数下标比前一个图形多3根,奇数下标比前一个图形多2根”.本题属于中档题型,有点难度,难点再与如何去寻找规律,做形如此类题型时,不妨将数据分成奇偶两组来讨论.

| A. | y3-y=y(y2-1) | B. | x2-x-3=x(x-1)-3 | C. | -m2+n2=-(m-n)(m+n) | D. | x2-3x+9=(x-3)2 |
| A. |  | B. |  | C. |  | D. |  |
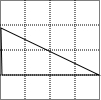
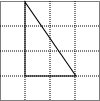
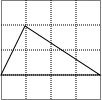
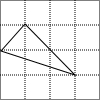 某同学在方格纸上画了四个三角形,与书本上的三角形(如图)相似的是( )
某同学在方格纸上画了四个三角形,与书本上的三角形(如图)相似的是( )
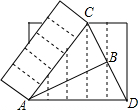 两张一边长相等的长方形纸片(AC=AD)如图放置,重合的顶点记为A,现将它们都分成5个宽度相等的长方形,点C是其中一条分割线与边的交点,连结CD与分割线交于点B,若AD=5,则△ABC的面积是5.
两张一边长相等的长方形纸片(AC=AD)如图放置,重合的顶点记为A,现将它们都分成5个宽度相等的长方形,点C是其中一条分割线与边的交点,连结CD与分割线交于点B,若AD=5,则△ABC的面积是5.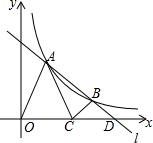 如图,直线l与双曲线$y=\frac{k}{x}$的一支相交于A、B两点,l与x轴相交于点D,C为线段OD中点,△OAC与△BCD分别是以OC、CD为底的等腰三角形,且S△OAC+S△BCD=2,则k=$\frac{3}{2}$.
如图,直线l与双曲线$y=\frac{k}{x}$的一支相交于A、B两点,l与x轴相交于点D,C为线段OD中点,△OAC与△BCD分别是以OC、CD为底的等腰三角形,且S△OAC+S△BCD=2,则k=$\frac{3}{2}$.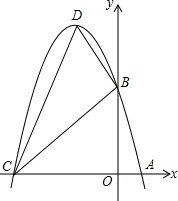 如图,抛物线y=-x2+bx+c与x轴交于点A、C,与y轴交于点B,它的顶点是D,对称轴是直线x=-2,且OB=OC.
如图,抛物线y=-x2+bx+c与x轴交于点A、C,与y轴交于点B,它的顶点是D,对称轴是直线x=-2,且OB=OC.