题目内容
13．
如图，矩形ABCD的对角线AC、BD相交于点O，CE∥BD，DE∥AC，若AC=4，则四边形OCED的周长为（ ）| A． | 4 | B． | 8 | C． | 10 | D． | 12 |
分析 由四边形ABCD为矩形，得到对角线互相平分且相等，得到OD=OC，再利用两对边平行的四边形为平行四边形得到四边形DECO为平行四边形，利用邻边相等的平行四边形为菱形得到四边形DECO为菱形，根据AC的长求出OC的长，即可确定出其周长．
解答 解：∵四边形ABCD为矩形，
∴OA=OC，OB=OD，且AC=BD，
∴OA=OB=OC=OD=2，
∵CE∥BD，DE∥AC，
∴四边形DECO为平行四边形，
∵OD=OC，
∴四边形DECO为菱形，
∴OD=DE=EC=OC=2，
则四边形OCED的周长为2+2+2+2=8，
故选B
点评 此题考查了矩形的性质，以及菱形的判定与性质，熟练掌握判定与性质是解本题的关键．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
3．
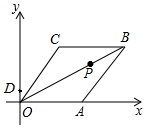已知菱形OABC在平面直角坐标系的位置如图所示，顶点A（5，0），OB=4$\sqrt{5}$，点P是对角线OB上的一个动点，D（0，1），当CP+DP最短时，点P的坐标为（ ）
已知菱形OABC在平面直角坐标系的位置如图所示，顶点A（5，0），OB=4$\sqrt{5}$，点P是对角线OB上的一个动点，D（0，1），当CP+DP最短时，点P的坐标为（ ）| A． | （0，0） | B． | （1，$\frac{1}{2}$） | C． | （$\frac{6}{5}$，$\frac{3}{5}$） | D． | （$\frac{10}{7}$，$\frac{5}{7}$） |
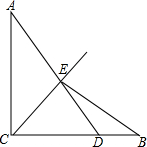如图，AC⊥BC，AC=BC，D是BC上一点，连接AD，与∠ACB的平分线交于点E，连接BE．若S△ACE=$\frac{6}{7}$，S△BDE=$\frac{3}{14}$，则AC=2．
如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别是A（2，2），B（4，0），C（4，-4）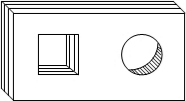
如图，是一个带有方形空洞和圆形空洞的儿童玩具，如果用下列几何体作为塞子，那么既可以堵住方形空洞，又可以堵住圆形空洞的几何体是（ ）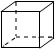
如图，⊙O的直径CD=20cm，AB是⊙O的弦，AB⊥CD，垂足为M，若OM=6cm，则AB的长为16cm．