题目内容
15. 如图,AB是⊙O的直径,AC、BC是⊙O的弦,直径DE⊥AC于点P.若点D在优弧$\widehat{ABC}$上,AB=8,BC=3,则DP=5.5.
如图,AB是⊙O的直径,AC、BC是⊙O的弦,直径DE⊥AC于点P.若点D在优弧$\widehat{ABC}$上,AB=8,BC=3,则DP=5.5.
分析 由AB和DE是⊙O的直径,可推出OA=OB=OD=4,∠C=90°,又有DE⊥AC,得到OP∥BC,于是有△AOP∽△ABC,根据相似三角形的性质即可得到结论.
解答 解:∵AB和DE是⊙O的直径,
∴OA=OB=OD=4,∠C=90°,
又∵DE⊥AC,
∴OP∥BC,
∴△AOP∽△ABC,
∴$\frac{OP}{BC}=\frac{AO}{AB}$,
即$\frac{OP}{3}=\frac{4}{8}$,
∴OP=1.5.
∴DP=OD+OP=5.5,
故答案为:5.5.
点评 本题主要考查了圆周角定理,平行线的判定,相似三角形的判定和性质,熟练掌握圆周角定理是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.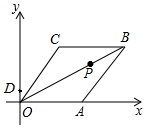 已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4$\sqrt{5}$,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )
已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4$\sqrt{5}$,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )
 已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4$\sqrt{5}$,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )
已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4$\sqrt{5}$,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )| A. | (0,0) | B. | (1,$\frac{1}{2}$) | C. | ($\frac{6}{5}$,$\frac{3}{5}$) | D. | ($\frac{10}{7}$,$\frac{5}{7}$) |
20. 秋季新学期开学时,红城中学对七年级新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格,现学校随机选取了部分学生的成绩,整理并制作成了如下不完整的图表:
秋季新学期开学时,红城中学对七年级新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格,现学校随机选取了部分学生的成绩,整理并制作成了如下不完整的图表:
请根据上述统计图表,解答下列问题:
(1)在表中,a=0.1,b=0.3,c=18;
(2)补全频数直方图;
(3)根据以上选取的数据,计算七年级学生的平均成绩.
(4)如果测试成绩不低于80分者为“优秀”等次,请你估计全校七年级的800名学生中,“优秀”等次的学生约有多少人?
 秋季新学期开学时,红城中学对七年级新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格,现学校随机选取了部分学生的成绩,整理并制作成了如下不完整的图表:
秋季新学期开学时,红城中学对七年级新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格,现学校随机选取了部分学生的成绩,整理并制作成了如下不完整的图表:| 分 数 段 | 频数 | 频率 |
| 60≤x<70 | 9 | a |
| 70≤x<80 | 36 | 0.4 |
| 80≤x<90 | 27 | b |
| 90≤x≤100 | c | 0.2 |
(1)在表中,a=0.1,b=0.3,c=18;
(2)补全频数直方图;
(3)根据以上选取的数据,计算七年级学生的平均成绩.
(4)如果测试成绩不低于80分者为“优秀”等次,请你估计全校七年级的800名学生中,“优秀”等次的学生约有多少人?
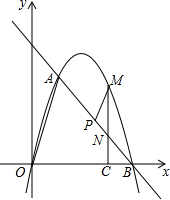 如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线y=mx2+nx相交于A(1,3$\sqrt{3}$),B(4,0)两点.
如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线y=mx2+nx相交于A(1,3$\sqrt{3}$),B(4,0)两点.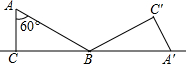 如图,△ABC中,∠C=90°,∠A=60°,AB=2$\sqrt{3}$.将△ABC沿直线CB向右作无滑动滚动一次,则点C经过的路径长是$\frac{5π}{2}$.
如图,△ABC中,∠C=90°,∠A=60°,AB=2$\sqrt{3}$.将△ABC沿直线CB向右作无滑动滚动一次,则点C经过的路径长是$\frac{5π}{2}$.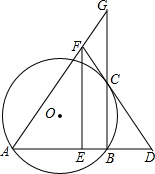 如图,已知:AB是⊙O的弦,过点B作BC⊥AB交⊙O于点C,过点C作⊙O的切线交AB的延长线于点D,取AD的中点E,过点E作EF∥BC交DC的延长线于点F,连接AF并延长交BC的延长线于点G.
如图,已知:AB是⊙O的弦,过点B作BC⊥AB交⊙O于点C,过点C作⊙O的切线交AB的延长线于点D,取AD的中点E,过点E作EF∥BC交DC的延长线于点F,连接AF并延长交BC的延长线于点G.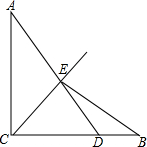 如图,AC⊥BC,AC=BC,D是BC上一点,连接AD,与∠ACB的平分线交于点E,连接BE.若S△ACE=$\frac{6}{7}$,S△BDE=$\frac{3}{14}$,则AC=2.
如图,AC⊥BC,AC=BC,D是BC上一点,连接AD,与∠ACB的平分线交于点E,连接BE.若S△ACE=$\frac{6}{7}$,S△BDE=$\frac{3}{14}$,则AC=2.