题目内容
10.因式分解(1)a3b-ab
(2)$\frac{1}{9}$x2-ax+$\frac{9}{4}$a2
(3)(p-4)(p+1)+3p
(4)x(x-y)2-2x2(y-x)
分析 (1)根据提公因式法和平方差公式可以对原式因式分解;
(2)根据完全平方公式可以对原式因式分解;
(3)先将原式展开,再根据平方差公式可以对原式因式分解;
(4)根据提公因式法可以对原式因式分解.
解答 解:(1)a3b-ab
=ab(a2-1)
=ab(a+1)(a-1);
(2)$\frac{1}{9}$x2-ax+$\frac{9}{4}$a2
=$\frac{1}{9}$$({x}^{2}-9ax+\frac{81}{4}{a}^{2})$
=$\frac{1}{9}(x-\frac{9}{2}a)^{2}$;
(3)(p-4)(p+1)+3p
=p2-3p-4+3p
=p2-4
=(p+2)(p-2);
(4)x(x-y)2-2x2(y-x)
=x(x-y)[(x-y)+2x]
=x(x-y)[x-y+2x]
=x(x-y)(3x-y).
点评 本题考查提公因式法与公式法的综合运用,解题的关键是针对相应的式子选取合适的方法进行因式分解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
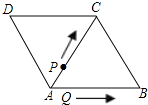 如图,△ABC和△ACD都是边长为2厘米的等边三角形,两个动点P,Q同时从A点出发,点P以0.5厘米/秒的速度沿A→C→B的方向运动,点Q以1厘米/秒的速度沿A→B→C→D的方向运动,当点Q运动到D点时,P、Q两点同时停止运动.设P、Q运动的时间为t秒
如图,△ABC和△ACD都是边长为2厘米的等边三角形,两个动点P,Q同时从A点出发,点P以0.5厘米/秒的速度沿A→C→B的方向运动,点Q以1厘米/秒的速度沿A→B→C→D的方向运动,当点Q运动到D点时,P、Q两点同时停止运动.设P、Q运动的时间为t秒