题目内容
19.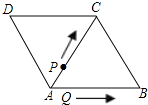 如图,△ABC和△ACD都是边长为2厘米的等边三角形,两个动点P,Q同时从A点出发,点P以0.5厘米/秒的速度沿A→C→B的方向运动,点Q以1厘米/秒的速度沿A→B→C→D的方向运动,当点Q运动到D点时,P、Q两点同时停止运动.设P、Q运动的时间为t秒
如图,△ABC和△ACD都是边长为2厘米的等边三角形,两个动点P,Q同时从A点出发,点P以0.5厘米/秒的速度沿A→C→B的方向运动,点Q以1厘米/秒的速度沿A→B→C→D的方向运动,当点Q运动到D点时,P、Q两点同时停止运动.设P、Q运动的时间为t秒(1)当t=2时,PQ=$\sqrt{3}$;
(2)求点P、Q从出发到相遇所用的时间;
(3)当t取何值时,△APQ是等边三角形;请说明理由;
(4)当P在线段AC上运动时,是否存在t使△APQ是直角三角形?若存在请直接写出t的值或t的取值范围,若不存在,请说明理由.
分析 (1)先求出AP,AQ的长度,再根据等边三角形的性质得到△APQ为直角三角形,利用勾股定理即可解答;
(2)△ABC是等边三角形,边长是2厘米.点P、Q从出发到相遇,即两人所走的路程的和是6cm.设从出发到相遇所用的时间是t秒.列方程就可以求出时间.
(3)当P在AC上,Q在AB上时,AP≠AQ,则一定不是等边三角形,当△APQ是等边三角形时,Q一定在边CD上,P一定在边CB上,若△APQ是等边三角形,则CP=DQ,根据这个相等关系,就可以得到一个关于t的方程,就可以得到t的值.
(4)P在线段AC上运动时,存在t使△APQ是直角三角形,t的取值范围:0<t<4.
解答 解:(1)当t=2时,AP=2×0.5=1厘米,AQ=2×1=2厘米,
如图1,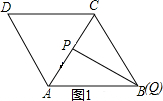
∵△ABC是边长为2厘米的等边三角形,
∴PQ⊥AC,
∴PQ=$\sqrt{A{B}^{2}-A{P}^{2}}=\sqrt{{2}^{2}-{1}^{2}}=\sqrt{3}$.
故答案为:$\sqrt{3}$.
(2)由0.5t+t=6,
解得t=4.
(3)当0≤t≤4时,都不存在;
当4<t≤6时,如图2,若△APQ是等边三角形,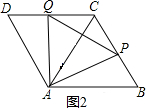
此时点P在BC上,点Q在CD上,且△ADQ≌△ACP,
则CP=DQ,
即6-t=0.5t-2,
解得:$t=\frac{16}{3}$.
(4)P在线段AC上运动时,存在t使△APQ是直角三角形,
t的取值范围:0<t<4.
点评 此题主要考查了等边三角形的判定与性质以及全等三角形的判定与性质,根据已知图形得出对应线段关系是解题关键.

练习册系列答案
相关题目
15.下列四个图形中,不一定是轴对称图形的是( )
| A. | 线段 | B. | 角 | C. | 直角三角形 | D. | 等边三角形 |
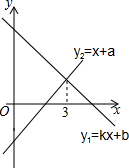 一次函数y1=kx+b与y2=x+a的图象如图,当y1>y2时,x的取值范围是x<3.
一次函数y1=kx+b与y2=x+a的图象如图,当y1>y2时,x的取值范围是x<3. 如图,在平面直角坐标系中,已知点A(0,8),点B(6,0),点P从B点以每秒1个单位的速度沿着BA方向出发,当点P运动到点A时停止,若设点P运动时间为t秒.
如图,在平面直角坐标系中,已知点A(0,8),点B(6,0),点P从B点以每秒1个单位的速度沿着BA方向出发,当点P运动到点A时停止,若设点P运动时间为t秒.