题目内容
6.解不等式组 $\left\{\begin{array}{l}{x-4<2(x-1)}\\{\frac{1+2x}{3}≥x}\end{array}\right.$,并把它的解集在数轴上表示出来.分析 首先分别计算出两个不等式的解集,再根据大小小大中间找确定不等式组的解集即可.
解答 解:$\left\{\begin{array}{l}{x-4<2(x-1)①}\\{\frac{1+2x}{3}≥x②}\end{array}\right.$,
不等式①的解集为:x>-2,
不等式②的解集为:x≤1,
∴原不等式组的解集为:-2<x≤1,
它的解集在数轴上表示为: .
.
点评 此题主要考查了解一元一次不等式组,以及在数轴上表示不等式的解集,把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.

练习册系列答案
相关题目
16.某篮球队5名主力队员的身高(单位:cm)分别是174,179,180,174,178,则这5名队员身高的中位数是( )
| A. | 174 | B. | 177 | C. | 178 | D. | 180 |
14. 如图,?ABCD中,AB=3,BC=5,AE平分∠BAD交BC于点E,则CE的长为
如图,?ABCD中,AB=3,BC=5,AE平分∠BAD交BC于点E,则CE的长为
( )
 如图,?ABCD中,AB=3,BC=5,AE平分∠BAD交BC于点E,则CE的长为
如图,?ABCD中,AB=3,BC=5,AE平分∠BAD交BC于点E,则CE的长为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
1.如图交通标志中,既是中心对称图形,又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
18.富豪阁社区为了解居民每月用于信息消费的金额,随机抽取了部分家庭进行调查,数据整理成如图所示的不完整统计图,已知A、B两组户数直方图的高度比为1:5,请结合图中相关数据回答下列问题.
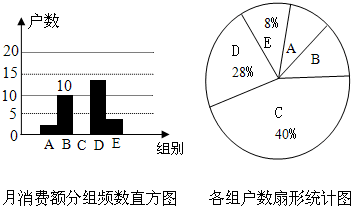
(1)A组的频数是2;本次调查样本的容量是50
(2)补全直方图(请标明各组频数);
(3)若该社区有1500户住户,请估计月信息消费额不少于300元的户数是多少?
月消费额分组统计图

(1)A组的频数是2;本次调查样本的容量是50
(2)补全直方图(请标明各组频数);
(3)若该社区有1500户住户,请估计月信息消费额不少于300元的户数是多少?
月消费额分组统计图
| 组别 | 消费额(元) |
| A | 10≤x<100 |
| B | 100≤x<200 |
| C | 200≤x<300 |
| D | 300≤x<400 |
| E | x>400 |
15.下列四个图形中,不一定是轴对称图形的是( )
| A. | 线段 | B. | 角 | C. | 直角三角形 | D. | 等边三角形 |
 已知:如图,在Rt△ABC中,O为斜边AC的中点,D为BC边上一点,过点A作
已知:如图,在Rt△ABC中,O为斜边AC的中点,D为BC边上一点,过点A作