题目内容
12.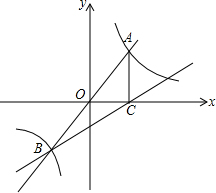 已知反比例函数y=$\frac{k}{x}$与直线y=x-1和直线y=2x三线相交于B,正比例函数y=2x与y=$\frac{k}{x}$相交于A,y=x-1交x轴于C,则S△ABC等于( )
已知反比例函数y=$\frac{k}{x}$与直线y=x-1和直线y=2x三线相交于B,正比例函数y=2x与y=$\frac{k}{x}$相交于A,y=x-1交x轴于C,则S△ABC等于( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 先求得交点B的坐标,进而根据A、B是中心对称点,求得A的坐标,由直线y=x-1求得C的坐标,即可根据S△ABC=S△AOC+S△BOC求得结果.
解答 解:∵直线y=x-1和直线y=2x相交于B,
∴$\left\{\begin{array}{l}{y=x-1}\\{y=2x}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$,
∴B(-1,-2),
∵反比例函数y=$\frac{k}{x}$经过点B,
∴k=-1×(-2)=2,
∴反比例函数为y=$\frac{2}{x}$,
∵正比例函数y=2x与y=$\frac{k}{x}$相交于A、B,且B(-1,-2),
∴A(1,2),
由直线y=x-1可知C(1,0),
∴S△ABC=S△AOC+S△BOC=$\frac{1}{2}$×1×2+$\frac{1}{2}$×1×2=2.
故选B.
点评 本题考查了反比例函数和一次函数的交点问题,求得交点坐标是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 如图,?ABCD中,对角线AC、BD相交于点O,点E是CD的中点,则△DOE与△BCD的面积比为1:4.
如图,?ABCD中,对角线AC、BD相交于点O,点E是CD的中点,则△DOE与△BCD的面积比为1:4.
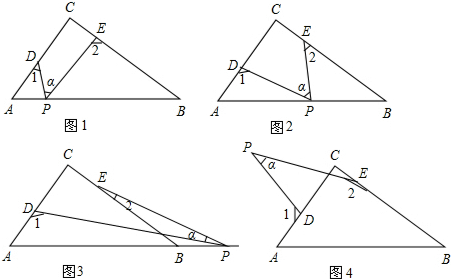
 如图,四边形ABCD是一个矩形,⊙C的半径是2,CF=4,EF=2,CE⊥EF于E,则图中阴影部分的面积为$\frac{4π}{3}$.
如图,四边形ABCD是一个矩形,⊙C的半径是2,CF=4,EF=2,CE⊥EF于E,则图中阴影部分的面积为$\frac{4π}{3}$. 如图,△ABC中,∠A=36°,BE平分∠ABC,CE平分∠ACD,求∠E的度数.
如图,△ABC中,∠A=36°,BE平分∠ABC,CE平分∠ACD,求∠E的度数.