题目内容
2.商场某种商品平均每天可销售30件,每件盈利50元,为了尽快减少库存,商场决定采取适当的降价措施,经调查发现,每件商品每降价1元,商场平均每天可多卖出2件.据此规律,每件商品降价多少元时,商场日盈利最大?最大利润是多少?分析 根据日盈利=每件商品盈利的钱数×(原来每天销售的商品件数30+2×降价的钱数),把相关数值代入求解即可,根据(1)得到的关系式判断出二次函数的对称轴,此时二次函数取到最值.
解答 解:(1)由题意得:(50-x)(30+2x)=2100,
化简得:x2-35x+300=0,
解得:x1=15,x2=20,
∵该商场为了尽快减少库存,则x=15不合题意,舍去.
∴x=20
答:每件商品降价20元,商场日盈利可达2100元;
(2)y=(50-x)(30+2x)=-2x2+70x+1500,
当x=-$\frac{b}{2a}$=17.5时,y最大.
答:每件商品降价17.5元时,商场日盈利的最大.
点评 此题主要考查了二次函数的应用;得到日盈利的等量关系是解决本题的关键.

练习册系列答案
相关题目
12.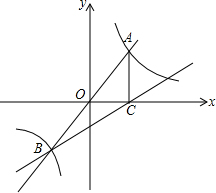 已知反比例函数y=$\frac{k}{x}$与直线y=x-1和直线y=2x三线相交于B,正比例函数y=2x与y=$\frac{k}{x}$相交于A,y=x-1交x轴于C,则S△ABC等于( )
已知反比例函数y=$\frac{k}{x}$与直线y=x-1和直线y=2x三线相交于B,正比例函数y=2x与y=$\frac{k}{x}$相交于A,y=x-1交x轴于C,则S△ABC等于( )
 已知反比例函数y=$\frac{k}{x}$与直线y=x-1和直线y=2x三线相交于B,正比例函数y=2x与y=$\frac{k}{x}$相交于A,y=x-1交x轴于C,则S△ABC等于( )
已知反比例函数y=$\frac{k}{x}$与直线y=x-1和直线y=2x三线相交于B,正比例函数y=2x与y=$\frac{k}{x}$相交于A,y=x-1交x轴于C,则S△ABC等于( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
11.下列计算中正确的是( )
| A. | $2\sqrt{3}+4\sqrt{2}=6\sqrt{5}$ | B. | $\sqrt{{{(-3)}^2}}=-3$ | C. | $\sqrt{27}÷\sqrt{3}=3$ | D. | $3\sqrt{3}×2\sqrt{2}=3\sqrt{6}$ |
12.下列四个几何体中,三视图都是中心对称图形的几何体是( )
| A. | 圆锥 | B. | 三棱柱 | C. | 圆柱 | D. | 五棱柱 |
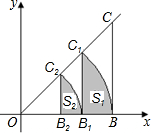 如图,已知,直线y=x上一点C,过C作CB⊥x轴于点B,B(4,0),以O为圆心,OB为半径作弧BC1,交OC于点C1,C1B1⊥OB于点B1,设弧BC1,C1B1,B1B围成的阴影部分的面积为S1,然后以O为圆心,OB1为半径作弧B1C2,交OC于点C2,C2B2⊥OB于点B2,设弧B1C2,C2B2,B2B1围成的阴影部分的面积为S2,则S2=π-2.
如图,已知,直线y=x上一点C,过C作CB⊥x轴于点B,B(4,0),以O为圆心,OB为半径作弧BC1,交OC于点C1,C1B1⊥OB于点B1,设弧BC1,C1B1,B1B围成的阴影部分的面积为S1,然后以O为圆心,OB1为半径作弧B1C2,交OC于点C2,C2B2⊥OB于点B2,设弧B1C2,C2B2,B2B1围成的阴影部分的面积为S2,则S2=π-2. 如图,是反比例函数$y=\frac{k-2}{x}$的图象的一个分支,对于给出的下列说法:
如图,是反比例函数$y=\frac{k-2}{x}$的图象的一个分支,对于给出的下列说法: