题目内容
10.已知点A(1,-3),B(4,-1),P(0,a),N(0,a-2),当四边形PABN的周长最小时,则a=-1.分析 如图,作点B关于y轴的对称点B′,则B′的坐标为(-4,-1),把B′向下平移2个单位得到点A'(-4,3),连接AA′,与y轴交于点N,把N向上平移2个单位得到P,于是得到PN=A′B′=2,推出四边形A′B′PN为平行四边形,根据平行四边形的性质得到PB′=A′N,PB=PB′,得到PB=NA′,于是推出PB+AN=AA′,此时PB+AN最小,而PN与AB的长一定,此时四边形ABDC的周长最短.由于A(1,-3),A′(-4,-3),得到AA′∥x轴,求得N(0,-3),即可得到结果.
解答  解:如图,作点B关于y轴的对称点B′,则B′的坐标为(-4,-1),把B′向下平移2个单位得到点A'(-4,3),连接AA′,与y轴交于点N,把N向上平移2个单位得到P,
解:如图,作点B关于y轴的对称点B′,则B′的坐标为(-4,-1),把B′向下平移2个单位得到点A'(-4,3),连接AA′,与y轴交于点N,把N向上平移2个单位得到P,
∴PN=A′B′=2,
∴A′B′∥PN,
∴四边形A′B′PN为平行四边形,
∴PB′=A′N,PB=PB′,
∴PB=NA′,
∴PB+AN=AA′,此时PB+AN最小,
而PN与AB的长一定,
∴此时四边形ABDC的周长最短.
∵A(1,-3),A′(-4,-3),∴AA′∥x轴,
∴N(0,-3),
∴P(0,-1).
∴a=-1.
故答案为:-1.
点评 本题考查了轴对称-最短路线问题:通过对称,把两条线段的和转化为一条线段,利用两点之间线段最短解决问题.也考查了坐标变换以及待定系数法求一次函数的解析式.

练习册系列答案
相关题目
20.下列运算正确的是( )
| A. | $\sqrt{16}$=±4 | B. | $\sqrt{4\frac{1}{9}}$=2$\frac{1}{3}$ | C. | $\sqrt{(2-\sqrt{5})^{2}}$=$\sqrt{5}$-2 | D. | (-$\sqrt{3}$)2=9 |
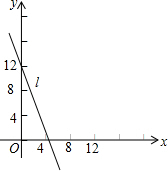 如图,直线l是一次函数y=kx+b的图象,观察图象可知:
如图,直线l是一次函数y=kx+b的图象,观察图象可知: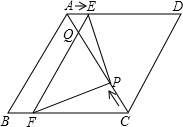 如图,在?ABCD中,AB=6cm,AD=AC=5cm,点P由C出发沿CA方向匀速运动,速度为1cm/s,同时,线段EF由AB出发沿AD方向匀速运动,速度为1cm/s,交AC于Q,连接PE、PF,若设运动时间为t(s)(0<t<5),解答下列问题:
如图,在?ABCD中,AB=6cm,AD=AC=5cm,点P由C出发沿CA方向匀速运动,速度为1cm/s,同时,线段EF由AB出发沿AD方向匀速运动,速度为1cm/s,交AC于Q,连接PE、PF,若设运动时间为t(s)(0<t<5),解答下列问题: