题目内容
在梯形ABCD中，AB∥CD，AB=a，CD=b，两腰延长线交于点M，过M作DC的平行线，分别交AC、BD延长线于E，F，则EF等于（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
考点：相似三角形的判定与性质
专题：
分析：根据已知可求得△MCD∽△MAB，从而求出BM：BD的值，又由△BCD∽△BEM，从而根据相似三角形的边对应边成比例求得EM的值，进而求得EF的值．
解答：解：∵AB∥CD，
∴△MDC∽△MBA，
∴
=
=
，
∴
=
，
在△BEM中，∵DC∥FM，
∴
=
，
∴EM=
=
，
同理，EM=FM，所以EF=
，
故选B．
∴△MDC∽△MBA，
∴
| MC |
| MA |
| CD |
| AB |
| b |
| a |
∴
| BM |
| BD |
| a |
| a-b |
在△BEM中，∵DC∥FM，
∴
| BD |
| BM |
| CD |
| EM |
∴EM=
| BM×CD |
| BD |
| ab |
| a-b |
同理，EM=FM，所以EF=
| 2ab |
| a-b |
故选B．
点评：此题主要考查平行线分线段成比例定理的理解及运用，主要考查学生的推理和计算能力．
练习册系列答案
华东师大版一课一练系列答案
孟建平名校考卷系列答案
相关题目
如图，点C、点D为线段AB的三等分点，则CD=
如图，已知MB=ND，∠MBA=∠NDC，下列哪个条件不能判定△ABM≌△CDN（ ）| A、∠M=∠N |
| B、AB=CD |
| C、AM=CN |
| D、AM∥CN |
如图，已知∠ACB=90°，AC=BC，BE⊥CE，AD⊥CE于点D，AD=2.5cm，DE=1.7cm，则BE=（ ）| A、1cm | B、0.8cm |
| C、4.2cm | D、1.5cm |
如图，点A、B、C在圆O上，∠A=60°，则∠BOC的度数是（ ）| A、15° | B、30° |
| C、60° | D、120° |
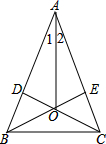已知：如图，CD⊥AB于D，BE⊥AC于E，CD、BE交于O，∠1=∠2．求证：OB=OC．