题目内容
8.在括号内填入适当的整式,使等式成立:(1)$\frac{2y}{x}$=$\frac{6xy}{()}$;
(2)$\frac{x}{x-y}$=$\frac{()}{{x}^{2}-{y}^{2}}$.
分析 (1)根据分式的分子分母都乘以(或除以)同一个不为零的整式,分式的值不变,可得答案;
(2)根据分式的分子分母都乘以(或除以)同一个不为零的整式,分式的值不变,可得答案.
解答 解:(1)分式的分子分母都乘以3x,得
$\frac{2y}{x}$=$\frac{6xy}{3{x}^{2}}$;
(2)分式的分子分母都乘以(x+y),得
$\frac{x}{x-y}$=$\frac{{x}^{2}+xy}{{x}^{2}-{y}^{2}}$,
故答案为:3x2,x2+xy.
点评 本题考查了分式的基本性质,利用了分式的基本性质:分式的分子分母都乘以(或除以)同一个不为零的整式,分式的值不变.

练习册系列答案
相关题目
19.若分式x2-12(x+1)的值等于0,则x的值为( )
| A. | 1 | B. | ±1 | C. | 12 | D. | -1 |
3.下列根式中,最简二次根式是( )
| A. | $\sqrt{25a}$ | B. | $\sqrt{{x}^{2}+{y}^{2}}$ | C. | $\sqrt{\frac{a}{2}}$ | D. | $\sqrt{0.7}$ |
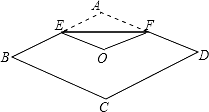 如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF,若菱形ABCD的边长为2cm,∠A=120°,则EF=$\sqrt{3}$cm.
如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF,若菱形ABCD的边长为2cm,∠A=120°,则EF=$\sqrt{3}$cm.