题目内容
16. 如图,已知一次函数y=kx-4k+5的图象与反比例函数y=$\frac{3}{x}$(x>0)的图象相交于点A(p,q).当一次函数y的值随x的值增大而增大时,p的取值范围是$\frac{3}{5}$<p<4.
如图,已知一次函数y=kx-4k+5的图象与反比例函数y=$\frac{3}{x}$(x>0)的图象相交于点A(p,q).当一次函数y的值随x的值增大而增大时,p的取值范围是$\frac{3}{5}$<p<4.
分析 先根据一次函数的解析式,得到一次函数y=kx-4k+5的图象经过点(4,5),过点(4,5)分别作y轴与x轴的垂线,分别交反比例函数图象于B点和C点,根据点A(p,q)只能在B点与C点之间,即可求得p的取值范围是$\frac{3}{5}$<p<4.
解答  解:一次函数y=kx-4k+5中,令x=4,则y=5,
解:一次函数y=kx-4k+5中,令x=4,则y=5,
故一次函数y=kx-4k+5的图象经过点(4,5),
如图所示,过点(4,5)分别作y轴与x轴的垂线,分别交反比例函数图象于B点和C点,
把y=5代入y=$\frac{3}{x}$,得x=$\frac{3}{5}$;
把x=4代入y=$\frac{3}{x}$,得y=$\frac{3}{4}$,
所以B点坐标为($\frac{3}{5}$,5),C点坐标为(4,$\frac{3}{4}$),
因为一次函数y的值随x的值增大而增大,
所以点A(p,q)只能在B点与C点之间的曲线上,
所以p的取值范围是$\frac{3}{5}$<p<4.
故答案为:$\frac{3}{5}$<p<4.
点评 本题考查了反比例函数图象与一次函数的交点问题:反比例函数与一次函数的图象的交点坐标满足两函数的解析式.解决问题的关键是确定点A在曲线上的位置.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.对于方程x2-2|x|+2=m,如果方程实根的个数为3个,则m的值等于( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2.5 |
1.我们知道:等腰三角形、平行四边形、菱形、双曲线、抛物线.这些都是我们在初中学习阶段学过的几何图形或函数的图象,那么从它们之中随机抽取两个,得到的都是中心对称图形的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{2}$ | D. | 1 |
5. 某校七年级有400名学生,在一次生物测验后,为了解本次测验的成绩情况,从中随机取了部分学生的成绩进行统计,并绘制了如下图表:
某校七年级有400名学生,在一次生物测验后,为了解本次测验的成绩情况,从中随机取了部分学生的成绩进行统计,并绘制了如下图表:
请你根据以上信息,解答下列问题:
(1)a=0.5,b=8,c=6,并补全条形统计图;
(2)请你估计该校七年级共有多少名学生本次成绩不低于80分;
(3)现从样本中的A等和D等学生中各随机选取一名同学组成互助学习小组,则直接写出两名同学恰好是一名男生和一名女生的概率.
 某校七年级有400名学生,在一次生物测验后,为了解本次测验的成绩情况,从中随机取了部分学生的成绩进行统计,并绘制了如下图表:
某校七年级有400名学生,在一次生物测验后,为了解本次测验的成绩情况,从中随机取了部分学生的成绩进行统计,并绘制了如下图表:| 等级 | 分数 | 频数 | 频率 |
| A | 90≤x≤100 | 6 | 0.15 |
| B | 80≤x<90 | 20 | a |
| C | 70≤x<80 | b | 0.2 |
| D | 60≤x<70 | c | 0.15 |
| 合计 | 1 |
(1)a=0.5,b=8,c=6,并补全条形统计图;
(2)请你估计该校七年级共有多少名学生本次成绩不低于80分;
(3)现从样本中的A等和D等学生中各随机选取一名同学组成互助学习小组,则直接写出两名同学恰好是一名男生和一名女生的概率.
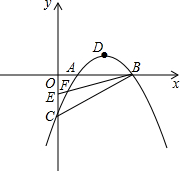 已知抛物线y=ax2+bx+c与x轴交于A(1,0),B(3,0),与y轴交于C(0,-2),顶点为D,点E的坐标为(0,-1),该抛物线于BE交于另一点F,连接BC
已知抛物线y=ax2+bx+c与x轴交于A(1,0),B(3,0),与y轴交于C(0,-2),顶点为D,点E的坐标为(0,-1),该抛物线于BE交于另一点F,连接BC