题目内容
1.对任意四个有理数a,b,c,d,定义新运算:$|{\begin{array}{l}a&b\\ c&d\end{array}}|=ad-bc$.(1)若$|{\begin{array}{l}{2x}&{-4}\\ x&1\end{array}}|=18$,则x=3;
(2)若$|{\begin{array}{l}{x+1}&2\\{x-1}&3\end{array}}|=|{\begin{array}{l}{2x}&5\\ 1&3\end{array}}|$,求x的值.
分析 (1)已知等式利用题中的新定义化简,求出解即可得到x的值;
(2)已知等式利用题中的新定义化简,求出解即可得到x的值.
解答 解:(1)根据题意化简得:2x+4x=18,
合并得:6x=18,
解得:x=3;
故答案为:(1)3;
(2)根据题意化简得:3(x+1)-2(x-1)=6x-5,
去括号得:3x+3-2x+2=6x-5,
移项合并得:5x=10,
解得:x=2.
点评 此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
6.代数式-$\frac{π}{7}$αb2的系数是( )
| A. | -7 | B. | -π | C. | -$\frac{π}{7}$ | D. | -$\frac{1}{7}$ |
11.用四舍五入法把3.1415926…精确到0.001得到的近似值是( )
| A. | 3.14 | B. | 3.142 | C. | 3.1416 | D. | 3.146 |
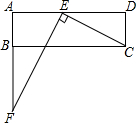 如图,在矩形ABCD中,已知AD>AB,在边AD上取点E,连结CE,过点E作EF⊥CE,与边AB的延长线交于点F.
如图,在矩形ABCD中,已知AD>AB,在边AD上取点E,连结CE,过点E作EF⊥CE,与边AB的延长线交于点F.