题目内容
12.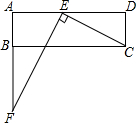 如图,在矩形ABCD中,已知AD>AB,在边AD上取点E,连结CE,过点E作EF⊥CE,与边AB的延长线交于点F.
如图,在矩形ABCD中,已知AD>AB,在边AD上取点E,连结CE,过点E作EF⊥CE,与边AB的延长线交于点F.(1)证明:△AEF∽△DCE.
(2)若AB=2,AE=3,AD=7,求线段AF的长.
分析 (1)由四边形ABCD为矩形,于是得到∠A=∠D=90°,根据垂直的定义得到∠AEF+∠DEC=90°,于是得到∠F=∠DEC,即可得到结论;
(2)由四边形ABCD为矩形,得到DC=AB=2,求出ED=AD-AE=4,根据相似三角形的性质得到$\frac{AF}{ED}=\frac{AE}{DC}$,代入数据即可得到结论.
解答 (1)证明:∵四边形ABCD为矩形,
∴∠A=∠D=90°,
∵CE⊥EF,
∴∠AEF+∠DEC=90°,
又∵∠F+∠AEF=90°,
∴∠F=∠DEC,
∴△AEF∽△DCE;
(2)解:∵四边形ABCD为矩形,
∴DC=AB=2,
∵AE=3,AD=7,
∴ED=AD-AE=4,
∵△AEF∽△DCE,
∴$\frac{AF}{ED}=\frac{AE}{DC}$,
∴$\frac{AF}{4}=\frac{3}{2}$,
∴AF=6.
点评 本题考查了相似三角形的判定和性质,矩形的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
20.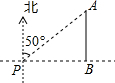 如图,一艘海轮位于灯塔P的北偏东50°方向,距离灯塔P为10海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向B处,那么海轮航行的距离AB的长是( )
如图,一艘海轮位于灯塔P的北偏东50°方向,距离灯塔P为10海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向B处,那么海轮航行的距离AB的长是( )
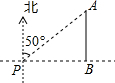 如图,一艘海轮位于灯塔P的北偏东50°方向,距离灯塔P为10海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向B处,那么海轮航行的距离AB的长是( )
如图,一艘海轮位于灯塔P的北偏东50°方向,距离灯塔P为10海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向B处,那么海轮航行的距离AB的长是( )| A. | 10海里 | B. | 10sin50°海里 | C. | 10cos50°海里 | D. | 10tan50°海里 |
17.一个矩形的周长为30,若矩形的一边长用字母x表示,则此矩形的面积为( )
| A. | x(15-x) | B. | x(30-x) | C. | x(30-2x) | D. | x(15+x) |
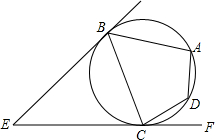 如图,EB,EC是⊙O的两条切线,与⊙O相切于B,C两点,点A,D在圆上.若∠E=46°,∠DCF=32°,则∠A的度数是99°.
如图,EB,EC是⊙O的两条切线,与⊙O相切于B,C两点,点A,D在圆上.若∠E=46°,∠DCF=32°,则∠A的度数是99°.