题目内容
15.用适当的方法解下列一元二次方程:(1)(x-1)2=4
(2)3x2-6x+4=0
(3)(x-2)(x-3)=12
(4)3y2+1=2$\sqrt{3}$y.
分析 (1)利用直接开平方法解方程;
(2)利用求根公式法解方程;
(3)先把方程化为一般式,然后利用因式分解法解方程;
(4)先把方程化为一般式,然后利用公式法解方程.
解答 解:(1)x-1=±2,
所以x1=3,x2=-1;.
(2)△=(-6)2-4×3×4=-12<0,
所以方程没有实数解;
(3)x2-5x-6=0,
(x-6)(x+1)=0,
所以x1=6,x2=-1;
(3)3y2-2$\sqrt{3}$y+1=0,
△=(-2$\sqrt{3}$)2-4×3×1=0,
y=$\frac{2\sqrt{3}±0}{2×3}$,
所以y1=y2=$\frac{\sqrt{3}}{3}$.
点评 本题考查了解一元二次方程-因式分解法:因式分解法就是利用因式分解求出方程的解的方法,这种方法简便易用,是解一元二次方程最常用的方法.也考查了公式法解一元二次方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5. 如图,已知a∥b,且∠2是∠1的2倍,那么∠2的度数为( )
如图,已知a∥b,且∠2是∠1的2倍,那么∠2的度数为( )
 如图,已知a∥b,且∠2是∠1的2倍,那么∠2的度数为( )
如图,已知a∥b,且∠2是∠1的2倍,那么∠2的度数为( )| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
6.对于二次函数 y=(x-1)2+2 的图象,下列说法正确的是( )
| A. | 开口向下 | B. | 顶点坐标是(-1,2) | ||
| C. | 对称轴是 x=1 | D. | 与 x 轴有两个交点 |
10.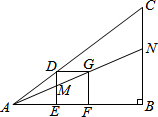 如图△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直线AG分别交DE、BC于M、N两点.若∠B=90°,AC=5,BC=3,DG=1,则BN的长度为( )
如图△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直线AG分别交DE、BC于M、N两点.若∠B=90°,AC=5,BC=3,DG=1,则BN的长度为( )
 如图△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直线AG分别交DE、BC于M、N两点.若∠B=90°,AC=5,BC=3,DG=1,则BN的长度为( )
如图△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直线AG分别交DE、BC于M、N两点.若∠B=90°,AC=5,BC=3,DG=1,则BN的长度为( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{8}{5}$ | D. | $\frac{12}{7}$ |
20.计算:$\frac{2x-6}{x-2}$÷$\frac{x-3}{{x}^{2}-4}$( )
| A. | 2x+4 | B. | 7 | C. | 5 | D. | 3 |
7.已知m是方程x2-x-2=0的一个根,则代数式m2-m+3=( )
| A. | -2 | B. | 1 | C. | 0 | D. | 5 |
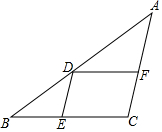 如图所示,在平行四边形DECF中,B是CE延长线上一点,BD的延长线交CF的延长线于点A.
如图所示,在平行四边形DECF中,B是CE延长线上一点,BD的延长线交CF的延长线于点A.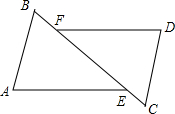 如图,AB=DC,BF=CE,需要补充一个条件,就能使△ABE≌△DCF,小明给出了四个答案::①AE=DF;②AE∥DF;③AB∥DC;④∠A=∠D,其中正确的是( )
如图,AB=DC,BF=CE,需要补充一个条件,就能使△ABE≌△DCF,小明给出了四个答案::①AE=DF;②AE∥DF;③AB∥DC;④∠A=∠D,其中正确的是( )