题目内容
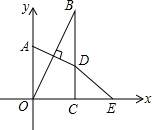已知，如图在直角坐标系中，点A在y轴上，BC⊥x轴于点C，点A关于直线OB的对称点D恰好在BC上，点E与点O关于直线BC对称，∠OBC=35°，则∠OED=考点：轴对称的性质,坐标与图形性质
专题：
分析：利用轴对称图形的性质得出∠OAD=∠ODA，∠DOE=∠DEO，进而得出∠B=∠AOB=35°，即可得出答案．
解答：
解：连接DO，
∵点A关于直线OB的对称点D恰好在BC上，点E与点O关于直线BC对称，
∴OA=OD，OD=DE，
∴∠OAD=∠ODA，∠DOE=∠DEO，
∵BC⊥x轴于点C，
∴AO∥BC，
∴∠B=∠AOB=35°，
∵AD⊥BO，AO=DO，
∴∠AOB=∠DOB=35°，
∴∠DOE=∠DEO=20°．
故答案为：20．
解：连接DO，∵点A关于直线OB的对称点D恰好在BC上，点E与点O关于直线BC对称，
∴OA=OD，OD=DE，
∴∠OAD=∠ODA，∠DOE=∠DEO，
∵BC⊥x轴于点C，
∴AO∥BC，
∴∠B=∠AOB=35°，
∵AD⊥BO，AO=DO，
∴∠AOB=∠DOB=35°，
∴∠DOE=∠DEO=20°．
故答案为：20．
点评：此题主要考查了轴对称图形的性质，正确把握轴对称的性质是解题关键．
练习册系列答案
名校课堂系列答案
相关题目
已知⊙O的半径为5，点P到圆心O的距离为3，则点P在（ ）
| A、圆内 | B、圆上 |
| C、圆外 | D、不能确定 |
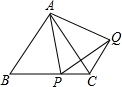如图，△ABC为等边三角形，P点在BC上，△APQ为等边三角形．求证：AB∥CQ．
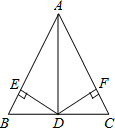如图，AD是BC的中垂线，DE⊥AB，DF⊥AC，垂足分别为E，F，说明下列结论的理由：
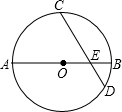如图，⊙O的直径AB=8，点C为弧AB的中点，E为OB上一点，∠AEC=60°，CE的延长线交⊙O于D，求弦CD的长．
