题目内容
13.(1)先化简($\frac{x}{x-5}$-$\frac{x}{5-x}$)÷$\frac{2x}{{x}^{2}-25}$,然后从不等式组$\left\{\begin{array}{l}{-x-2≤3}\\{2x<12}\end{array}\right.$的解集中,选取一个你认为符合题意的x的值代入求值.(2)先化简,再求值:$\frac{a-b}{a}$÷(a-$\frac{2ab-{b}^{2}}{a}$),然后给a,b选择一个你喜欢的数代入求值.
分析 (1)先根据分式混合运算的法则把原式进行化简,再求出不等式组$\left\{\begin{array}{l}{-x-2≤3}\\{2x<12}\end{array}\right.$的解集,选取符合题意的x的值代入求值即可;
(2)先根据分式混合运算的法则把原式进行化简,再选取合适的a、b的值代入进行计算即可.
解答 解:(1)原式=$\frac{2x}{x-5}$•$\frac{(x+5)(x-5)}{2x}$
=x+5,
解不等式组$\left\{\begin{array}{l}{-x-2≤3}\\{2x<12}\end{array}\right.$得,-5≤x<6,
当x=1时,原式=6.
(2)原式=$\frac{a-b}{a}$÷$\frac{{a}^{2}-2ab+{b}^{2}}{a}$
=$\frac{a-b}{a}$•$\frac{a}{(a-b)^{2}}$
=$\frac{1}{a-b}$,
当a=2,b=1时,原式=$\frac{1}{2-1}$=1.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
2.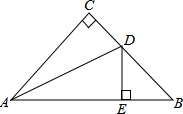 如图,∠C=90°,AC=BC,AD平分∠CAB,交BC于D,DE⊥AB于E,且AB=6cm,则△DEB周长为( )
如图,∠C=90°,AC=BC,AD平分∠CAB,交BC于D,DE⊥AB于E,且AB=6cm,则△DEB周长为( )
 如图,∠C=90°,AC=BC,AD平分∠CAB,交BC于D,DE⊥AB于E,且AB=6cm,则△DEB周长为( )
如图,∠C=90°,AC=BC,AD平分∠CAB,交BC于D,DE⊥AB于E,且AB=6cm,则△DEB周长为( )| A. | 4cm | B. | 6cm | C. | 10cm | D. | 14cm |
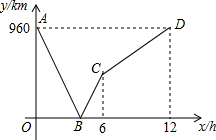 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发.设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据题中所给信息解答以下问题:
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发.设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据题中所给信息解答以下问题: