题目内容
7.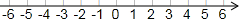 (1)计算:(-2015)0+2-2-($\frac{3}{2}$)2+|3.14-π|
(1)计算:(-2015)0+2-2-($\frac{3}{2}$)2+|3.14-π|(2)解不等式组$\left\{\begin{array}{l}{1-2(x-1)>x\\;①}\\{\frac{x-1}{3}≥\frac{x+1}{4}-1\\;②}\end{array}\right.$把解集在数轴上表示出来,并求它的整数解.
分析 (1)根据零指数幂,负整数指数幂,有理数的乘方,绝对值分别求出每一部分的值,再代入求出即可;
(2)求出每一不等式的解集,再求出不等式组的解集即可.
解答 解:(1)原式=1+$\frac{1}{4}$-$\frac{9}{4}$+π-3.14
=π-4.14;
(2)∵解不等式①得:x<1,
解不等式②得:x≥-5,
∴不等式组的解集为-5≤x<1,
在数轴上表示不等式组的解集为: ,
,
不等式组的整数解为-5,-4,-3,-2,-1,0.
点评 本题考查了解一元一次不等式组,在数轴上表示不等式组的解集,不等式组的整数解,零指数幂,负整数指数幂,有理数的乘方,绝对值的应用,能正确利用所学的知识点进行计算是解此题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
15.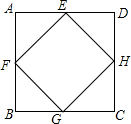 如图,点E、F、G、H是正方形ABCD各边的中点,则四边形EFGH( )
如图,点E、F、G、H是正方形ABCD各边的中点,则四边形EFGH( )
 如图,点E、F、G、H是正方形ABCD各边的中点,则四边形EFGH( )
如图,点E、F、G、H是正方形ABCD各边的中点,则四边形EFGH( )| A. | 是轴对称图形但不是中心对称图形 | B. | 既是轴对称图形又是中心对称图形 | ||
| C. | 是中心对称图形但不是轴对称图形 | D. | 没有对称性 |
19.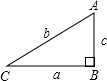 如图,在直角三角形ABC中,∠B=90°,以下式子成立的是( )
如图,在直角三角形ABC中,∠B=90°,以下式子成立的是( )
 如图,在直角三角形ABC中,∠B=90°,以下式子成立的是( )
如图,在直角三角形ABC中,∠B=90°,以下式子成立的是( )| A. | a2+b2=c2 | B. | a2+c2=b2 | C. | b2+c2=a2 | D. | (a+c)2=b2 |
16.代数式$\frac{\sqrt{x-5}}{x-6}$有意义,则x的取值范围是( )
| A. | x≤5 | B. | x≥5 | C. | x>5且x≠6 | D. | x≥5且x≠6 |
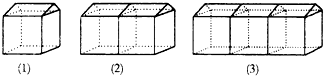 搭建如图(1)的单顶帐篷需要17根钢管,这样的帐篷按图(2)、(3)的方式串起来搭建,则串8顶这样的帐篷需要94根钢管.
搭建如图(1)的单顶帐篷需要17根钢管,这样的帐篷按图(2)、(3)的方式串起来搭建,则串8顶这样的帐篷需要94根钢管.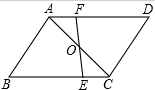 如图,在?ABCD中,O是对角线AC的中点,过点O的直线EF分别交点BC、AD于点E、F.证明:
如图,在?ABCD中,O是对角线AC的中点,过点O的直线EF分别交点BC、AD于点E、F.证明: