题目内容
2.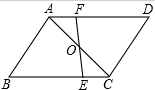 如图,在?ABCD中,O是对角线AC的中点,过点O的直线EF分别交点BC、AD于点E、F.证明:
如图,在?ABCD中,O是对角线AC的中点,过点O的直线EF分别交点BC、AD于点E、F.证明:(1)△AOF≌△COE;
(2)BE=DF.
分析 (1)根据平行四边形的性质得到AD∥BC,于是得到∠FAC=∠BCA,∠AFE=∠CEF,AO=CO于是证得结论;
(2)根据全等三角形的性质即可得到结论.
解答 证明:(1)在平行四边形ABCD中,
∵AD∥BC,
∴∠FAC=∠BCA,∠AFE=∠CEF,
又∵AO=CO,
在△AOF与△COF中$\left\{\begin{array}{l}{∠FAC=∠BCF}\\{∠AFE=∠CEF}\\{AO=CO}\end{array}\right.$,
∴△AOF≌△COE;
(2)由(1)知△AOF≌△COF;
∴AF=CE,
又∵AD=BC,
∴AD-AF=BC-BE,
即BE=DF.
点评 本题考查了平行四边形的性质及全等三角形的判定,解答本题需要掌握两点,①平行四边形的对边相等且平行,②全等三角形的对应边、对应角分别相等.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
12.下列事件是必然事件的是( )
| A. | 抛一枚硬币反面朝上 | |
| B. | 明天是晴天 | |
| C. | 打开电视正在播放新闻 | |
| D. | 袋中有两个黄球,任意摸出一球是黄球 |
17. 如图,在△ABC中,D、E分别是边AB、AC的中点,若BC=6,则DE的长为( )
如图,在△ABC中,D、E分别是边AB、AC的中点,若BC=6,则DE的长为( )
 如图,在△ABC中,D、E分别是边AB、AC的中点,若BC=6,则DE的长为( )
如图,在△ABC中,D、E分别是边AB、AC的中点,若BC=6,则DE的长为( )| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
14.下列计算正确的是( )
| A. | (a-b)2=(a+b)(a-b) | B. | (a2)3=a5 | C. | (-a)2•(-a)3=-a5 | D. | (ab)3=ab3 |
11.“中国汉字听写大会”是由中央电视台和国家语言文字工作委员会联合主办的节目,希望通过节目的播出,能吸引更多的人关注对汉字文化的学习.某校也开展了一次“汉字听写”比赛,每位参赛学生听写40个汉字.比赛结束后随机抽取部分学生的听写结果,按听写正确的汉字个数x绘制成了以下不完整的统计图.
根据以上信息回答下列问题:
(1)本次共随机抽取了50名学生进行调查,听写正确的汉字个数x在21≤x<31范围的人数最多;
(2)补全频数分布直方图;
(3)各组的组中值如下表所示.若用各组的组中值代表各组每位学生听写正确的汉字个数,求被调查学生听写正确的汉字个数的平均数;
(4)该校共有1350名学生,如果听写正确的汉字个数不少于21个定为良好,请你估计该校本次“汉字听写”比赛达到良好的学生人数.

根据以上信息回答下列问题:
(1)本次共随机抽取了50名学生进行调查,听写正确的汉字个数x在21≤x<31范围的人数最多;
(2)补全频数分布直方图;
(3)各组的组中值如下表所示.若用各组的组中值代表各组每位学生听写正确的汉字个数,求被调查学生听写正确的汉字个数的平均数;
| 听写正确的汉字个数x | 组中值 |
| 1≤x<11 | 6 |
| 11≤x<21 | 16 |
| 21≤x<31 | 26 |
| 31≤x<41 | 36 |
 (1)求证:等腰三角形底边中点到两腰的距离相等.
(1)求证:等腰三角形底边中点到两腰的距离相等.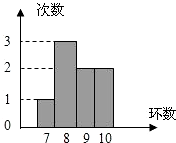 一名射击运动员连续打靶8次,命中的环数如图所示,这组数据的众数是8.
一名射击运动员连续打靶8次,命中的环数如图所示,这组数据的众数是8. (1)计算:(-2015)0+2-2-($\frac{3}{2}$)2+|3.14-π|
(1)计算:(-2015)0+2-2-($\frac{3}{2}$)2+|3.14-π|