��Ŀ����
3�� ��֪����ABC��ƽ��ֱ������ϵ�е�λ����ͼ����ʾ��A������Ϊ��-6��0����B������Ϊ��4��0������DΪBC���е㣬��EΪ�߶�AB��һ���㣮������A��B��C����������ߵĽ���ʽΪy=ax2+bx+8��
��֪����ABC��ƽ��ֱ������ϵ�е�λ����ͼ����ʾ��A������Ϊ��-6��0����B������Ϊ��4��0������DΪBC���е㣬��EΪ�߶�AB��һ���㣮������A��B��C����������ߵĽ���ʽΪy=ax2+bx+8����1���������ߵĽ���ʽΪy=-$\frac{1}{3}$x2-$\frac{2}{3}$x+8��
��2������AD����F����������A��C֮���һ�㣬ֱ��BF��AD�ڵ�P������PE����BP+PE��ֵ��Сʱ��д����ʱ��F�����꣨-$\frac{15}{4}$��$\frac{93}{16}$����
���� ��1����A��B������������y=ax2+bx+8�����ô���ϵ����������ã�
��2���ɣ�1����֪AB=AC�����֪PB=PC�����֪PB+PE=PC+PE�����֪P��C��E���㹲�ߣ�ҪʹPC+PE��С����PE��AB����O���E�غϣ����������Сֵ����G��GH��x���ڵ�H���ɡ�COB�ס�AOP�����OP������PO��GH������ƽ���߷��߶γɱ��������GH�������G�������꣬�ٴ��������߽���ʽ�����G�����ꣻ
��� 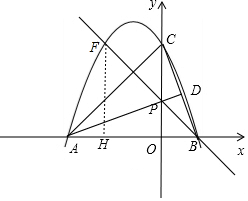 �⣺��1����A��B������������y=ax2+bx+8�ã�$\left\{\begin{array}{l}{36a-6b+8=0}\\{16a+4b+8=0}\end{array}\right.$��
�⣺��1����A��B������������y=ax2+bx+8�ã�$\left\{\begin{array}{l}{36a-6b+8=0}\\{16a+4b+8=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=-\frac{1}{3}}\\{b=-\frac{2}{3}}\end{array}\right.$��
�������ߵĽ���ʽΪy=-$\frac{1}{3}$x2-$\frac{2}{3}$x+8��
�ʴ�Ϊy=-$\frac{1}{3}$x2-$\frac{2}{3}$x+8��
��2����y=ax2+bx+8��֪C��0��8����
��A��������-6��0����B��������4��0����
��OA=6��OC=8��OB=4��
��AB=10��AC=$\sqrt{{6}^{2}+{8}^{2}}$=10��
��AB=AC��
��DΪBC���е㣬
��ADΪ�߶�BC�Ĵ�ֱƽ���ߣ�
��BP=PC��
��BP+PE=PC+PE��
Ҫʹ����С��P��C��E���㹲�ߣ�
��BP+PE=CE
ҪʹCE��С����CE��AB����ʱ��O���E�غϣ�
��BP+PE=OC=8����BP+PE����СֵΪ8��
��ͼ����F��FH��x���ڵ�H����F��x��-$\frac{1}{3}$x2-$\frac{2}{3}$x+8�������֪x��0��
��BH=4-x��FH=-$\frac{1}{3}$x2-$\frac{2}{3}$x+8��
�ߡ�DPO+��DBO=��APO+��DPO=180�㣬
���APO=��CBO���ҡ�AOP=��COB=90�㣬
���AOP�ס�COB��
��$\frac{AO}{CO}$=$\frac{OP}{OB}$����$\frac{6}{8}$=$\frac{OP}{4}$�����OP=3��
��FH��OP��
��$\frac{OP}{FH}$=$\frac{OB}{BH}$����$\frac{3}{-\frac{1}{3}{x}^{2}-\frac{2}{3}x+8}$=$\frac{4}{4-x}$�����x=4����ȥ����x=-$\frac{15}{4}$��
��F��������-$\frac{15}{4}$��$\frac{93}{16}$����
�ʴ�Ϊ��-$\frac{15}{4}$��$\frac{93}{16}$����
���� ����Ϊ���κ������ۺ�Ӧ�ã��漰����ϵ��������κ����Ľ���ʽ�����������ε��ж������ʡ����ɶ��������������ε��ж������ʼ�����˼���֪ʶ���ڣ�2����ȷ����PB+PE��СʱE���λ���ǽ���Ĺؼ���

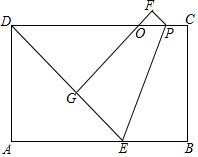 ��ͼ���ھ���ABCD�У�AD=a��AB=b��E��AB����һ�㣬��AE=AD��P���߶�CD��һ�㣬����PE������������PE�۵�����B��C�ֱ�����G��F����FG��CD���ڵ�O��
��ͼ���ھ���ABCD�У�AD=a��AB=b��E��AB����һ�㣬��AE=AD��P���߶�CD��һ�㣬����PE������������PE�۵�����B��C�ֱ�����G��F����FG��CD���ڵ�O��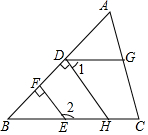 ��ͼ���ڡ�ABC�У���E��H��BC�ϣ�EF��AB��HD��AB������ֱ���F��D����G��AC�ϣ���AGD=��ACB����˵����1+��2=180�㣮
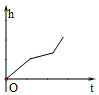
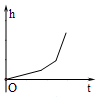
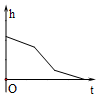
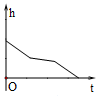
��ͼ���ڡ�ABC�У���E��H��BC�ϣ�EF��AB��HD��AB������ֱ���F��D����G��AC�ϣ���AGD=��ACB����˵����1+��2=180�㣮 ��ͼ�����ٵ����������עˮ����������ע������עˮ������������Һ��ĸ߶�h��ʱ��t�仯�ĺ���ͼ����ӽ�ʵ��������ǣ�������
��ͼ�����ٵ����������עˮ����������ע������עˮ������������Һ��ĸ߶�h��ʱ��t�仯�ĺ���ͼ����ӽ�ʵ��������ǣ�������