题目内容
8.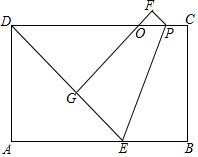 如图,在矩形ABCD中,AD=a,AB=b,E是AB边上一点,且AE=AD,P是线段CD上一点,连结PE,将矩形沿着PE折叠,点B,C分别落在G,F处,FG,CD交于点O.
如图,在矩形ABCD中,AD=a,AB=b,E是AB边上一点,且AE=AD,P是线段CD上一点,连结PE,将矩形沿着PE折叠,点B,C分别落在G,F处,FG,CD交于点O.(1)当点G正好落在线段DE上,
①求证:DP=DE;
②当a=5,b=10时,求△FOP的周长.
(2)若a=6,b=6+2$\sqrt{3}$,当点P从点C移动到点D时,请求出点G经过的路径长.
分析 (1)①依据矩形的性质和平行线的性质可证明∠DPE=∠BEP,由翻折的性质得到∠BEP=∠GEP,则∠DPE=∠GEP,最后利用等角对等边的性质进行证明即可;②先依据勾股定理求得DE的长,然后依据翻折的性质可得GE的长,从而可得到DG的长,依据OF=FG-OG可得到OF的长,接下来证明△DGO、△OFP为等腰直角三角形,最后依据△FOP的周长=(2+$\sqrt{2}$)OF求解即可;
(2)由翻折的性质可知BE=EG=2$\sqrt{3}$,点G在以E为圆心,以EG为半径的圆弧上,然后求得当点P与点C重合,点P与点D重合时,GE与G′E所组成的夹角的度数,最后依据扇形的弧长公式求解即可.
解答 解:(1)①∵ABCD为矩形,
∴DC∥AB.
∴∠DPE=∠BEP.
由翻折的性质可知:∠BEP=∠GEP.
∴∠DPE=∠GEP.
∴DP=DE.
②∵在Rt△ADE中,AD=AE=5,
∴DE=5$\sqrt{2}$,∠ADE=45°.
由折叠的性质可知:EG=EB=5,∠FGE=∠B=90°.
∴DG=DE-GE=5$\sqrt{2}$-5.
∵∠GDO=45°,∠DGO=90°,
∴△DGO为等腰直角三角形.
∴OG=DG=5$\sqrt{2}$-5.
由折叠的性质可知:GF=BC=5.
∴OF=5-(5$\sqrt{2}$-5)=10-5$\sqrt{2}$.
∵∠FOP=45°,∠F=90°,
∴△FOP为等腰直角三角形.
∴△FOP的周长=OF+PF+OP=(2+$\sqrt{2}$)OF=(2+$\sqrt{2}$)(10-5$\sqrt{2}$)=10.
(2)∵AD=AE=6,AB=6+2$\sqrt{3}$,
∴BE=2$\sqrt{3}$.
由翻折的性质可知BE=EG=2$\sqrt{3}$.
∴点G在以E为圆心,以EG为半径的圆弧上.
当点P与点C重合时,tan∠PEB=$\frac{PB}{EB}$=$\frac{6}{2\sqrt{3}}$=$\sqrt{3}$.
∴∠PEB=60°.
由翻折的性质可知∠BEG=2∠PEB=120°.
∴∠GEA=60°.
当点P′与点D重合时,∠P′EB=135°.
由翻折的性质可知:∠P′EG′=135°.
∴∠AEG′=90°.
∴∠GEG′=60°+90°=150°.
∴点G运动的路径=$\frac{150π×(2\sqrt{3})^{2}}{360}$=5π.
点评 本题主要考查的是四边形的综合应用,解答本题主要应用了矩形的性质、翻折的性质、特殊锐角三角函数值的应用,扇形的弧长公式,求得∠GEG′的度数是解题的关键.

| A. | 3cm,4cm,8cm | B. | 17cm,7cm,9cm | C. | 12cm,14cm,20cm | D. | 5cm,5cm,11cm |
| A. |  | B. |  | C. |  | D. |  |
 如图,正方形AOBC的两边在坐标轴上,D是OB的中点,直线CD的函数关系式为y=2x-6,则△CDE的面积为6.(平方单位)
如图,正方形AOBC的两边在坐标轴上,D是OB的中点,直线CD的函数关系式为y=2x-6,则△CDE的面积为6.(平方单位) 已知,△ABC在平面直角坐标系中的位置如图①所示,A点坐标为(-6,0),B点坐标为(4,0),点D为BC的中点,点E为线段AB上一动点.经过点A、B、C三点的抛物线的解析式为y=ax2+bx+8.
已知,△ABC在平面直角坐标系中的位置如图①所示,A点坐标为(-6,0),B点坐标为(4,0),点D为BC的中点,点E为线段AB上一动点.经过点A、B、C三点的抛物线的解析式为y=ax2+bx+8.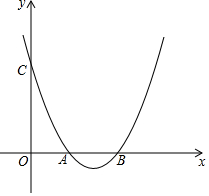 已知:抛物线y=ax2+bx+c与x轴交于点A(2,0)、B(4,0),且过点C(0,4).
已知:抛物线y=ax2+bx+c与x轴交于点A(2,0)、B(4,0),且过点C(0,4).