题目内容
10. 如图,在三角形ABC中,已知AB=AC,D为BC边上的一点,且AB=BD,AD=CD,则∠ABC等于( )
如图,在三角形ABC中,已知AB=AC,D为BC边上的一点,且AB=BD,AD=CD,则∠ABC等于( )| A. | 36° | B. | 38° | C. | 40° | D. | 45° |
分析 根据等腰三角形的性质得到∠B=∠C,根据三角形外角的性质得到∠ADB=2∠C=2∠B,于是得到∠BDA=∠BAD=2∠B,在△ABD中利用三角形内角和定理可求出∠B.
解答 解:∵AB=AC,
∴∠B=∠C,
∵CD=DA,
∴∠C=∠DAC,
∵BA=BD,
∴∠BDA=∠BAD=2∠C=2∠B,
又∵∠B+∠BAD+∠BDA=180°,
∴5∠B=180°,
∴∠B=36°,
故选A.
点评 本题主要考查等腰三角形的性质,掌握等边对等角是解题的关键,注意三角形内角和定理和方程思想的应用.

练习册系列答案
相关题目
18. 如图,在等腰△ABC中,AB=AC,∠A=20°,AB上一点D使AD=BC,过点D作DE∥BC且DE=AB,连接EC,则∠DCE的度数为( )
如图,在等腰△ABC中,AB=AC,∠A=20°,AB上一点D使AD=BC,过点D作DE∥BC且DE=AB,连接EC,则∠DCE的度数为( )
 如图,在等腰△ABC中,AB=AC,∠A=20°,AB上一点D使AD=BC,过点D作DE∥BC且DE=AB,连接EC,则∠DCE的度数为( )
如图,在等腰△ABC中,AB=AC,∠A=20°,AB上一点D使AD=BC,过点D作DE∥BC且DE=AB,连接EC,则∠DCE的度数为( )| A. | 80° | B. | 70° | C. | 60° | D. | 45° |
15.已知△ABC∽△DEF,且AB:DE=1:2,则△ABC与△DEF的周长之比为( )
| A. | 1:2 | B. | 2:1 | C. | 1:4 | D. | 4:3 |
20. 我们在制作视力表时发现,每个“E”形图的长和宽相等(即每个“E”形图近似于正方形),如图,小明在制作视力表时,测得l1=14cm,l2=7cm,他选择了一张面积为4cm2的正方形卡纸,刚好可以剪得第②个小“E”形图.那么下面四张正方形卡纸中,能够刚好剪得第①个大“E”形图的是( )
我们在制作视力表时发现,每个“E”形图的长和宽相等(即每个“E”形图近似于正方形),如图,小明在制作视力表时,测得l1=14cm,l2=7cm,他选择了一张面积为4cm2的正方形卡纸,刚好可以剪得第②个小“E”形图.那么下面四张正方形卡纸中,能够刚好剪得第①个大“E”形图的是( )
 我们在制作视力表时发现,每个“E”形图的长和宽相等(即每个“E”形图近似于正方形),如图,小明在制作视力表时,测得l1=14cm,l2=7cm,他选择了一张面积为4cm2的正方形卡纸,刚好可以剪得第②个小“E”形图.那么下面四张正方形卡纸中,能够刚好剪得第①个大“E”形图的是( )
我们在制作视力表时发现,每个“E”形图的长和宽相等(即每个“E”形图近似于正方形),如图,小明在制作视力表时,测得l1=14cm,l2=7cm,他选择了一张面积为4cm2的正方形卡纸,刚好可以剪得第②个小“E”形图.那么下面四张正方形卡纸中,能够刚好剪得第①个大“E”形图的是( )| A. | 面积为8cm2的卡纸 | B. | 面积为16cm2的卡纸 | ||
| C. | 面积为32cm2的卡纸 | D. | 面积为64cm2的卡纸 |
 在△ABC中,∠B=2∠C,AC=4$\sqrt{5}$,AB=5,求BC的长.
在△ABC中,∠B=2∠C,AC=4$\sqrt{5}$,AB=5,求BC的长.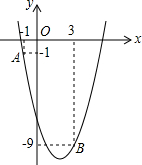 如图,已知二次函数y=ax2-4x+c的图象经过点A(-1,-1)和点B(3,-9).
如图,已知二次函数y=ax2-4x+c的图象经过点A(-1,-1)和点B(3,-9).