题目内容
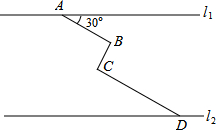 如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号).
如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号).考点:解直角三角形的应用
专题:几何图形问题
分析:过B点作BE⊥l1,交l1于E,CD于F,l2于G.在Rt△ABE中,根据三角函数求得BE,在Rt△BCF中,根据三角函数求得BF,在Rt△DFG中,根据三角函数求得FG,再根据EG=BE+BF+FG即可求解.
解答: 解:过B点作BE⊥l1,交l1于E,CD于F,l2于G.
解:过B点作BE⊥l1,交l1于E,CD于F,l2于G.
在Rt△ABE中,BE=AB•sin30°=20×
=10km,
在Rt△BCF中,BF=BC÷cos30°=10÷
=
km,
CF=BF•sin30°=
×
=
km,
DF=CD-CF=(30-
)km,
在Rt△DFG中,FG=DF•sin30°=(30-
)×
=(15-
)km,
∴EG=BE+BF+FG=(25+5
)km.
故两高速公路间的距离为(25+5
)km.
 解:过B点作BE⊥l1,交l1于E,CD于F,l2于G.
解:过B点作BE⊥l1,交l1于E,CD于F,l2于G.在Rt△ABE中,BE=AB•sin30°=20×
| 1 |
| 2 |
在Rt△BCF中,BF=BC÷cos30°=10÷
| ||
| 2 |
20
| ||
| 3 |
CF=BF•sin30°=
20
| ||
| 3 |
| 1 |
| 2 |
10
| ||
| 3 |
DF=CD-CF=(30-
10
| ||
| 3 |
在Rt△DFG中,FG=DF•sin30°=(30-
10
| ||
| 3 |
| 1 |
| 2 |
5
| ||
| 3 |
∴EG=BE+BF+FG=(25+5
| 3 |
故两高速公路间的距离为(25+5
| 3 |
点评:此题考查了解直角三角形的应用,主要是三角函数的基本概念及运算,关键把实际问题转化为数学问题加以计算.

练习册系列答案
相关题目
计算2x(3x2+1),正确的结果是( )
| A、5x3+2x |
| B、6x3+1 |
| C、6x3+2x |
| D、6x2+2x |
 如图,AD、BC相交于O,OA=OC,∠OBD=∠ODB.求证:AB=CD.
如图,AD、BC相交于O,OA=OC,∠OBD=∠ODB.求证:AB=CD.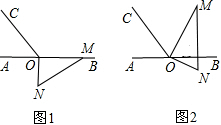 如图1,点O为直线AB上一点,过O点作直线OC,使∠BOC=120°,将一块 含30°,60°的直角三角板的直角顶点放在O处,一边OM在射线OB上,另一边ON在直线AB下方.
如图1,点O为直线AB上一点,过O点作直线OC,使∠BOC=120°,将一块 含30°,60°的直角三角板的直角顶点放在O处,一边OM在射线OB上,另一边ON在直线AB下方.
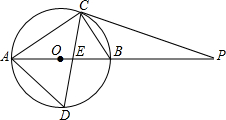 如图,⊙O的直径AB为10cm,弦BC为5cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.
如图,⊙O的直径AB为10cm,弦BC为5cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.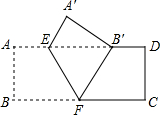 如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是
如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是