题目内容
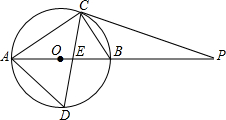 如图,⊙O的直径AB为10cm,弦BC为5cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.
如图,⊙O的直径AB为10cm,弦BC为5cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.(1)求AC、AD的长;
(2)试判断直线PC与⊙O的位置关系,并说明理由.
考点:切线的判定,勾股定理,圆周角定理
专题:几何综合题
分析:(1)连接BD,先求出AC,在Rt△ABC中,运用勾股定理求AC,②由CD平分∠ACB,得出AD=BD,所以Rt△ABD是直角等腰三角形,求出AD,
(2)连接OC,由角的关系求出∠PCB=∠ACO,可得到∠OCP=90°,所以直线PC与⊙O相切.
(2)连接OC,由角的关系求出∠PCB=∠ACO,可得到∠OCP=90°,所以直线PC与⊙O相切.
解答: 解:(1)①如图,连接BD,
解:(1)①如图,连接BD,
∵AB是直径,
∴∠ACB=∠ADB=90°,
在Rt△ABC中,
AC=
=
=5
(cm),
②∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴
=
,
∴AD=BD,
∴Rt△ABD是直角等腰三角形,
∴AD=
AB=
×10=5
cm;
(2)直线PC与⊙O相切,
理由:连接OC,
 ∵OC=OA,
∵OC=OA,
∴∠CAO=∠OCA,
∵PC=PE,
∴∠PCE=∠PEC,
∵∠PEC=∠CAE+∠ACE,
∵CD平分∠ACB,
∴∠ACE=∠ECB,
∴∠PCB=∠CAO=∠ACO,
∵∠ACB=90°,
∴∠OCP=∠OCB+∠PCB=∠ACO+∠OCB=∠ACB=90°,
即OC⊥PC,
∴直线PC与⊙O相切.
 解:(1)①如图,连接BD,
解:(1)①如图,连接BD,∵AB是直径,
∴∠ACB=∠ADB=90°,
在Rt△ABC中,
AC=
| AB2-BC2 |
| 102-52 |
| 3 |
②∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴
 |
| AD |
 |
| BD |
∴AD=BD,
∴Rt△ABD是直角等腰三角形,
∴AD=
| ||
| 2 |
| ||
| 2 |
| 2 |
(2)直线PC与⊙O相切,
理由:连接OC,
 ∵OC=OA,
∵OC=OA,∴∠CAO=∠OCA,
∵PC=PE,
∴∠PCE=∠PEC,
∵∠PEC=∠CAE+∠ACE,
∵CD平分∠ACB,
∴∠ACE=∠ECB,
∴∠PCB=∠CAO=∠ACO,
∵∠ACB=90°,
∴∠OCP=∠OCB+∠PCB=∠ACO+∠OCB=∠ACB=90°,
即OC⊥PC,
∴直线PC与⊙O相切.
点评:本题主要考查了切线的判定,勾股定理和圆周角,解题的关键是运圆周角和角平分线及等腰三角形正确找出相等的角.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
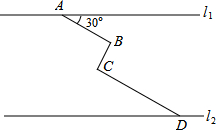 如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号).
如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号).
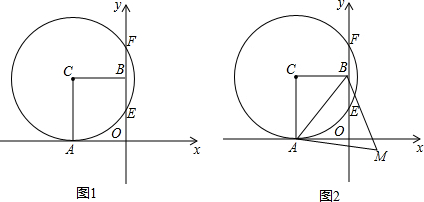

 如图,函数y=
如图,函数y=