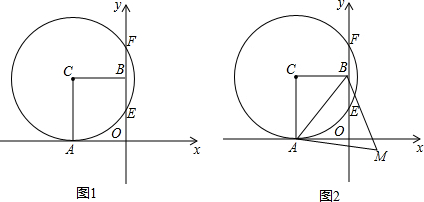题目内容
已知二次函数y=x2-4x+3.
(1)用配方法求其图象的顶点C的坐标,并描述该函数的函数值随自变量的增减而变化的情况;
(2)求函数图象与x轴的交点A,B的坐标,及△ABC的面积.
(1)用配方法求其图象的顶点C的坐标,并描述该函数的函数值随自变量的增减而变化的情况;
(2)求函数图象与x轴的交点A,B的坐标,及△ABC的面积.
考点:抛物线与x轴的交点,二次函数的性质,二次函数的三种形式
专题:数形结合
分析:(1)配方后求出顶点坐标即可;
(2)求出A、B的坐标,根据坐标求出AB、CD,根据三角形面积公式求出即可.
(2)求出A、B的坐标,根据坐标求出AB、CD,根据三角形面积公式求出即可.
解答:解:(1)y=x2-4x+3
=x2-4x+4-4+3
=(x-2)2-1,
所以顶点C的坐标是(2,-1),
当x<2时,y随x的增大而减少;
当x>2时,y随x的增大而增大;
(2)解方程x2-4x+3=0
得:x1=3,x2=1,
即A点的坐标是(1,0),B点的坐标是(3,0),
过C作CD⊥AB于D,

∵AB=2,CD=1,
∴S△ABC=
AB×CD=
×2×1=1.
=x2-4x+4-4+3
=(x-2)2-1,
所以顶点C的坐标是(2,-1),
当x<2时,y随x的增大而减少;
当x>2时,y随x的增大而增大;
(2)解方程x2-4x+3=0
得:x1=3,x2=1,
即A点的坐标是(1,0),B点的坐标是(3,0),
过C作CD⊥AB于D,

∵AB=2,CD=1,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了抛物线与x轴的交点,二次函数的性质,二次函数的三种形式的应用,主要考查学生运用性质进行计算的能力,题目比较典型,难度适中.

练习册系列答案
相关题目
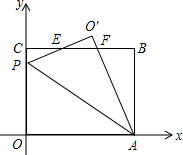 在平面直角坐标系中,O是坐标原点,矩形OABC的位置如图所示,点A,C的坐标分别为(10,0),(0,8).点P是y轴上的一个动点,将△OAP沿AP翻折得到△O′AP,直线BC与直线O′P交于点E,与直线O′A交于点F.
在平面直角坐标系中,O是坐标原点,矩形OABC的位置如图所示,点A,C的坐标分别为(10,0),(0,8).点P是y轴上的一个动点,将△OAP沿AP翻折得到△O′AP,直线BC与直线O′P交于点E,与直线O′A交于点F.
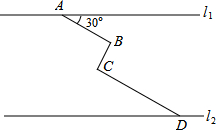 如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号).
如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号).