题目内容
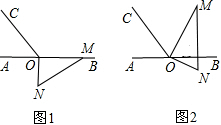 如图1,点O为直线AB上一点,过O点作直线OC,使∠BOC=120°,将一块 含30°,60°的直角三角板的直角顶点放在O处,一边OM在射线OB上,另一边ON在直线AB下方.
如图1,点O为直线AB上一点,过O点作直线OC,使∠BOC=120°,将一块 含30°,60°的直角三角板的直角顶点放在O处,一边OM在射线OB上,另一边ON在直线AB下方.(1)将图1中的三角板绕点O按逆时针方向旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.问:直线ON是否平分∠AOC?请说明理由.
(2)将图1中的三角板绕点O按每秒6°的速度逆时针方向旋转一周.
①若旋转到某一时刻,使ON在∠AOC的内部,且∠AOM=3∠NOC,求旋转时间t的值.
②在旋转过程中,直线MN∥直线OC时,求旋转时间t的值.
考点:角的计算,角平分线的定义
专题:
分析:(1)由角的平分线的定义和等角的余角相等求解;
(2)①根据角之间的关系求出∠CON=15°,进而求出旋转角等于225°.
②由∠BOC=120°可得∠AOC=60°,则∠RON=30°,即旋转90°或270°时ON平分∠AOC,据此求解;
(2)①根据角之间的关系求出∠CON=15°,进而求出旋转角等于225°.
②由∠BOC=120°可得∠AOC=60°,则∠RON=30°,即旋转90°或270°时ON平分∠AOC,据此求解;
解答:解:(1)直线ON平分∠AOC.
理由:如图2,
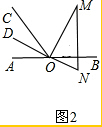
设ON的反向延长线为OD,
∵OM平分∠BOC,
∴∠MOC=∠MOB,
又∵OM⊥ON,
∴∠MOD=∠MON=90°,
∴∠COD=∠BON,
又∵∠AOD=∠BON(对顶角相等),
∴∠COD=∠AOD,
∴OD平分∠AOC
即直线ON平分∠AOC.
(2)①如图3,
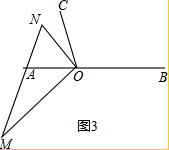
ON在∠AOC的内部,且∠AOM=3∠NOC,
∵∠AOM+∠AON=90°,∠CON+∠AON=60°,
∴∠AOM-∠CON=30°,
∴∠CON=15°,旋转角为225°,
故t=
=37.5(秒).
②如图
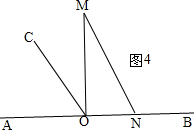
如图4:
∵MN∥OC,
∴∠M=∠COM=30°,
∴∠BOM=90°,
即旋转角为90°,
∴t=90÷6=15(秒)
如图5:

∵MN∥OC,
∴∠ONM=∠AOC=60°
∴点N在AB上
∴旋转角为270°
∴t=270÷6=45(秒)
即t的值为:
=15(秒)或
=45(秒).
理由:如图2,

设ON的反向延长线为OD,
∵OM平分∠BOC,
∴∠MOC=∠MOB,
又∵OM⊥ON,
∴∠MOD=∠MON=90°,
∴∠COD=∠BON,
又∵∠AOD=∠BON(对顶角相等),
∴∠COD=∠AOD,
∴OD平分∠AOC
即直线ON平分∠AOC.
(2)①如图3,

ON在∠AOC的内部,且∠AOM=3∠NOC,
∵∠AOM+∠AON=90°,∠CON+∠AON=60°,
∴∠AOM-∠CON=30°,
∴∠CON=15°,旋转角为225°,
故t=
| 225 |
| 6 |
②如图

如图4:
∵MN∥OC,
∴∠M=∠COM=30°,
∴∠BOM=90°,
即旋转角为90°,
∴t=90÷6=15(秒)
如图5:

∵MN∥OC,
∴∠ONM=∠AOC=60°
∴点N在AB上
∴旋转角为270°
∴t=270÷6=45(秒)
即t的值为:
| 90 |
| 6 |
| 270 |
| 6 |
点评:此题考查了角平分线的定义,应该认真审题并仔细观察图形,找到各个量之间的关系,是解题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
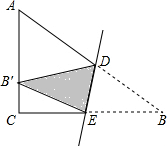 在Rt△ABC中,∠C=90°,AC=6,BC=8,将△BDC沿直线DE折叠,使B落在AC的三等分点B′处,求CE的长.
在Rt△ABC中,∠C=90°,AC=6,BC=8,将△BDC沿直线DE折叠,使B落在AC的三等分点B′处,求CE的长.
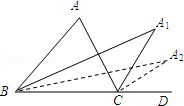 如图,在△ABC中,∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;…∠A2013BC与∠A2013CD的平分线相交于点A2014,得∠A2014,根据题意填空:
如图,在△ABC中,∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;…∠A2013BC与∠A2013CD的平分线相交于点A2014,得∠A2014,根据题意填空: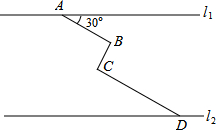 如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号).
如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号).

 如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形
如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形