题目内容
5.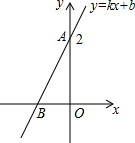 如图所示,直线AB是一次函数y=kx+b的图象.若AB=$\sqrt{5}$,则函数解析式为y=2x+2.
如图所示,直线AB是一次函数y=kx+b的图象.若AB=$\sqrt{5}$,则函数解析式为y=2x+2.
分析 先利用勾股定理计算出OB的长,从而得到B点坐标,然后把A点和B点坐标代入y=kx+b得到关于k、b的方程组,再解方程组求出k、b即可得到一次函数解析式.
解答 解:在Rt△AOB中,OB=$\sqrt{A{B}^{2}-O{A}^{2}}$=$\sqrt{(\sqrt{5})^{2}-{2}^{2}}$=1,则B(-1,0),
把A(0,2),B(-1,0)代入y=kx+b得$\left\{\begin{array}{l}{b=2}\\{-k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=2}\\{b=2}\end{array}\right.$,
所以函数解析式为y=2x+2.
故答案为y=2x+2.
点评 本题考查了待定系数法求一次函数解析式:先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;再将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;然后解方程或方程组,求出待定系数的值,进而写出函数解析式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.函数y=2x+4的图象与x轴,y轴的交点为A,B,若AB=2$\sqrt{5}$.则原点O到AB的距离是( )
| A. | $\sqrt{5}$ | B. | $\frac{4\sqrt{5}}{5}$ | C. | 2$\sqrt{5}$ | D. | $\frac{2\sqrt{5}}{3}$ |
14.从长度分别为2,4,6,7的四条线段中随机取三条,能构成三角形的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
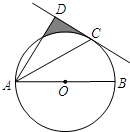 如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.若AB=$2\sqrt{6}$,∠BAC=30°,则图中阴影部分的面积为$\frac{9\sqrt{3}}{4}$-π.
如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.若AB=$2\sqrt{6}$,∠BAC=30°,则图中阴影部分的面积为$\frac{9\sqrt{3}}{4}$-π.