题目内容
5. 如图,直线y=2x+3与x轴交于点A,与y轴交于点B,D是射线AB上的动点(不与点A重合),DN⊥x轴于N,把△AND沿直线AB翻折,得到△AMD,延长MA交y轴于点C,过A、C、D三点的圆E与x轴交于点F,连结DF.
如图,直线y=2x+3与x轴交于点A,与y轴交于点B,D是射线AB上的动点(不与点A重合),DN⊥x轴于N,把△AND沿直线AB翻折,得到△AMD,延长MA交y轴于点C,过A、C、D三点的圆E与x轴交于点F,连结DF.(1)直接写出tan∠BAO的值为2;
(2)求证:MC=NF;
(3)求线段OC的长;
(4)是否存在点D,使DF∥AC?若存在,求点D的坐标;若不存在,请说明理由.
分析 (1)根据三角函数的定义即刻得到结论;
(2)连接DC,则∠MCD=∠NFD,根据全等三角形的性质即刻得到结论;
(3)作CG⊥y轴于G,根据平行线的性质得到∠AGC=∠DAF,等量代换得到∠AGC=∠GAC,求得GC=AC,设GC=a,根据三角函数的定义得到BC=2a,求得OC=2a-3,根据勾股定理即刻得到结论;
(4)设D(m,2m+3)当DF∥AC时,∠DFA=∠FAC,根据三角函数的定义得到DN=2m+3,求得NF=$\frac{3}{4}$(2m+3),列方程即刻得到结论.
解答 解:(1)在y=2x+3中,令y=0,得x=-$\frac{3}{2}$,令x=0,得y=3,
∴A(-$\frac{3}{2}$,0),B(0,3),
∴OA=$\frac{3}{2}$,OB=3,
∴tan∠BAO=$\frac{OB}{OA}$=2;
故答案为:2;
(2)连接DC,则∠MCD=∠NFD,
在△MCD与△DNF中,$\left\{\begin{array}{l}{∠MCD=∠NFD}\\{∠DMC=∠DNF}\\{DM=DN}\end{array}\right.$,
∴△MCD≌△NFD,
∴MC=NF;
(3)作CG⊥y轴于G,
∵CG∥x轴,
∴∠AGC=∠DAF,
∵∠GAC=∠MAD=∠DAF,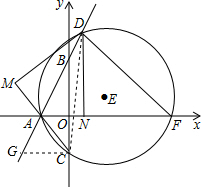
∴∠AGC=∠GAC,
∴GC=AC,
设GC=a,
∵tan∠BAO=tan∠BGC=2,
∴BC=2a,
∴OC=2a-3,
∵AO2+OC2=AC2,
∴1.52+(2a-3)2=a2,
解得:a=$\frac{5}{2}$,a=$\frac{3}{2}$(舍去),
∴线段OC的长是2;
(4)存在,理由:设D(m,2m+3)
当DF∥AC时,∠DFA=∠FAC,
由(3)知,tan∠CAO=$\frac{OC}{OA}=\frac{4}{3}$,
∴tan∠DFA=$\frac{4}{3}$,
∵DN=2m+3,
∴NF=$\frac{3}{4}$(2m+3),
∵MA=AN=$\frac{3}{2}$+m,AC=$\sqrt{O{A}^{2}+O{C}^{2}}$=$\frac{5}{2}$,
∴NF=MC=AC+AM=$\frac{3}{2}$+m+$\frac{5}{2}$=4+m=$\frac{3}{4}$(2m+3),
解得:m=$\frac{7}{2}$,
∴存在点D($\frac{7}{2}$,10).
点评 本题考查了全等三角形的判断和性质,勾股定理,平行线的判定和性质,三角函数的定义,圆周角定理,正确的作出辅助线是解题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | -3a2b2 | B. | -3ab | C. | -3a2b | D. | -3a3b3 |
| A. | 6月14日晚上能看到月亮 | |
| B. | 早晨的太阳从东方升起 | |
| C. | 打开初三数学书本,正好翻到第21页 | |
| D. | 任意掷一枚均匀的硬币,正面朝上 |
 如图,某中学制作了学生拓展性课程中选择棋类、球类、美术、书法四门课程情况的扇形统计图,从图中可以看出选择书法的学生的百分比为10%.
如图,某中学制作了学生拓展性课程中选择棋类、球类、美术、书法四门课程情况的扇形统计图,从图中可以看出选择书法的学生的百分比为10%.