题目内容
14.在一个不透明的袋子里,有2个黑球和1个白球,除了颜色外全部相同,任意摸两个球,摸到1黑1白的概率是$\frac{2}{3}$.分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与所摸到1黑1白的情况,再利用概率公式即可求得答案.
解答 解:依题意画树状图得:
∵共有6种等可能的结果,所摸到的球恰好为1黑1白的有4种情况,
∴所摸到的球恰好为1黑1白的概率是:$\frac{4}{6}$=$\frac{2}{3}$.
故答案为:$\frac{2}{3}$.
点评 本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.解题时注意:概率=所求情况数与总情况数之比.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
4.如表是一个4×4(4行4列共16个“数”组成)的奇妙方阵,从这个方阵中选四个“数”,而且这四个“数”中的任何两个不在同一行,也不在同一列,有很多选法,把每次选出的四个“数”相加,其和是定值,则方阵中第三行三列的“数”是( )
| 30 | $\sqrt{4}$ | 2$\sqrt{3}$sin60° | 22 |
| -3 | -2 | -$\sqrt{2}$sin45° | 0 |
| |-5| | 6 | 23 | |
| ($\frac{1}{3}$)-1 | 4 | $\sqrt{25}$ | ($\frac{1}{6}$)-1 |
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
2.-2的倒数是( )
| A. | 2 | B. | -2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
6.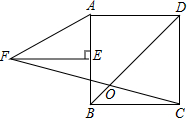 如图,正方形ABCD中,E为AB中点,FE⊥AB,AF=2AE,FC交BD于O,则∠DOC的度数为( )
如图,正方形ABCD中,E为AB中点,FE⊥AB,AF=2AE,FC交BD于O,则∠DOC的度数为( )
 如图,正方形ABCD中,E为AB中点,FE⊥AB,AF=2AE,FC交BD于O,则∠DOC的度数为( )
如图,正方形ABCD中,E为AB中点,FE⊥AB,AF=2AE,FC交BD于O,则∠DOC的度数为( )| A. | 60° | B. | 67.5° | C. | 75° | D. | 54° |
19.若点A(a,-2)、B(4,b)在正比例函数y=kx的图象上,则下列等式一定成立的是( )
| A. | a-b=6 | B. | a+b=-10 | C. | a•b=-8 | D. | $\frac{a}{b}$=-2 |
 一副三角尺按如图的位置摆放(顶点C 与F 重合,边CA与边FE叠合,顶点B、C、D在一条直线上).将三角尺DEF绕着点F按顺时针方向旋转n°后(0<n<180 ),如果EF∥AB,那么n的值是45.
一副三角尺按如图的位置摆放(顶点C 与F 重合,边CA与边FE叠合,顶点B、C、D在一条直线上).将三角尺DEF绕着点F按顺时针方向旋转n°后(0<n<180 ),如果EF∥AB,那么n的值是45.
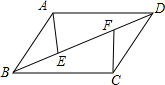 如图所示,已知点E,F在?ABCD的对角线BD上,且BF=DE,求证:AE=CF.
如图所示,已知点E,F在?ABCD的对角线BD上,且BF=DE,求证:AE=CF.