题目内容
16.如果任意选择一对有序整数(m,n),其中|m|≤1,|n|≤3,每一对这样的有序整数被选择的可能性是相等的,那么关于x的方程x2+nx+m=0有两个相等实数根的概率是$\frac{1}{7}$.分析 首先确定m、n的值,推出有序整数(m,n)共有:3×7=21(种),由方程x2+nx+m=0有两个相等实数根,则需:△=n2-4m=0,有(0,0),(1,2),(1,-2)三种可能,由此即可解决问题、
解答 解:m=0,±1,n=0,±1,±2,±3
∴有序整数(m,n)共有:3×7=21(种),
∵方程x2+nx+m=0有两个相等实数根,则需:△=n2-4m=0,有(0,0),(1,2),(1,-2)三种可能,
∴关于x的方程x2+nx+m=0有两个相等实数根的概率是$\frac{3}{21}$=$\frac{1}{7}$,
故答案为$\frac{1}{7}$.
点评 此题考查了概率、根的判别式以及根与系数的关系、绝对值不等式等知识,此题难度适中,注意掌握概率=所求情况数与总情况数之比.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
4.如表是一个4×4(4行4列共16个“数”组成)的奇妙方阵,从这个方阵中选四个“数”,而且这四个“数”中的任何两个不在同一行,也不在同一列,有很多选法,把每次选出的四个“数”相加,其和是定值,则方阵中第三行三列的“数”是( )
| 30 | $\sqrt{4}$ | 2$\sqrt{3}$sin60° | 22 |
| -3 | -2 | -$\sqrt{2}$sin45° | 0 |
| |-5| | 6 | 23 | |
| ($\frac{1}{3}$)-1 | 4 | $\sqrt{25}$ | ($\frac{1}{6}$)-1 |
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
1.下列运算正确的是( )
| A. | a2•a3=a6 | B. | a8÷a2=a4 | C. | (a3)2=a5 | D. | (ab)2=a2b2 |
8.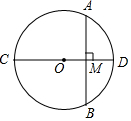 如图,CD为⊙O的直径,弦AB⊥CD,垂足为M,若AB=12,OM:MD=5:8,则⊙O的周长为( )
如图,CD为⊙O的直径,弦AB⊥CD,垂足为M,若AB=12,OM:MD=5:8,则⊙O的周长为( )
 如图,CD为⊙O的直径,弦AB⊥CD,垂足为M,若AB=12,OM:MD=5:8,则⊙O的周长为( )
如图,CD为⊙O的直径,弦AB⊥CD,垂足为M,若AB=12,OM:MD=5:8,则⊙O的周长为( )| A. | 26π | B. | 13π | C. | $\frac{96π}{5}$ | D. | $\frac{39\sqrt{10}π}{5}$ |
6.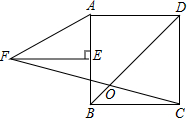 如图,正方形ABCD中,E为AB中点,FE⊥AB,AF=2AE,FC交BD于O,则∠DOC的度数为( )
如图,正方形ABCD中,E为AB中点,FE⊥AB,AF=2AE,FC交BD于O,则∠DOC的度数为( )
 如图,正方形ABCD中,E为AB中点,FE⊥AB,AF=2AE,FC交BD于O,则∠DOC的度数为( )
如图,正方形ABCD中,E为AB中点,FE⊥AB,AF=2AE,FC交BD于O,则∠DOC的度数为( )| A. | 60° | B. | 67.5° | C. | 75° | D. | 54° |
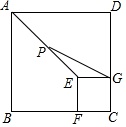 如图,正方形ABCD和正方形EFCG的边长分别为3和1,点F,G分别在边BC,CD上,P为AE的中点,连接PG,则PG的长为$\sqrt{5}$.
如图,正方形ABCD和正方形EFCG的边长分别为3和1,点F,G分别在边BC,CD上,P为AE的中点,连接PG,则PG的长为$\sqrt{5}$.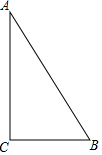 如图,在Rt△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为( )
如图,在Rt△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为( )