题目内容
19. 如图,抛物线y=ax2+2x+c经过点A(0,3),B(-1,0),请解答下列问题.
如图,抛物线y=ax2+2x+c经过点A(0,3),B(-1,0),请解答下列问题.(1)求抛物线的解析式;
(2)抛物线的顶点为点D,对称轴与x轴交于点E,连接BD,求BD的长.
(3)写出把抛物线先向上平移2个单位,再向右平移3个单位的函数解析式.
分析 (1)把点A(0,3),B(-1,0)代入抛物线y=ax2+2x+c,建立方程组求得a、c即可;
(2)化为顶点式求得抛物线的顶点坐标,得出点E坐标,利用勾股定理求得BD的长;
(3)利用平移的规律和顶点式得出平移后的规律即可.
解答 解:(1)把点A(0,3),B(-1,0)代入抛物线y=ax2+2x+c得
$\left\{\begin{array}{l}{c=3}\\{a-2+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-1}\\{c=3}\end{array}\right.$.
所以抛物线的解析式y=-x2+2x+3;
(2)y=-x2+2x+3=-(x-1)2+4,
顶点D的坐标为(1,4),点E坐标为(1,0),
则BD=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$;
(3)把抛物线先向上平移2个单位,再向右平移3个单位的函数解析式y=-(x-1-3)2+4+2=-(x-4)2+6.
点评 此题考查待定系数法求函数解析式,抛物线的平移规律,勾股定理,掌握待定系数法是解决问题的关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
7.三角形的外心具有的性质是( )
| A. | 到三边的距离相等 | B. | 外心一定在三角形外 | ||
| C. | 到三个顶点的距离相等 | D. | 外心一定在三角形内 |
14.抛物线y=x2-4x-4的对称轴是( )
| A. | x=-2 | B. | x=2 | C. | x=4 | D. | x=-4 |
9.将抛物线y=3x2如何平移得到抛物线y=3(x-5)2+1( )
| A. | 向左平移5个单位,向下平移1个单位 | |
| B. | 向左平移5个单位,向上平移1个单位 | |
| C. | 向右平移5个单位,向下平移1个单位 | |
| D. | 向右平移5个单位,向上平移1个单位 |
 如图,在平面直角坐标系中,P是∠1的边OA上一点,点P的坐标为(3,4),则tan∠1的值为$\frac{4}{3}$.
如图,在平面直角坐标系中,P是∠1的边OA上一点,点P的坐标为(3,4),则tan∠1的值为$\frac{4}{3}$.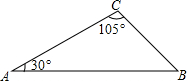 如图,已知AC=8,∠A=30°,∠C=105°,求AB和BC的长.
如图,已知AC=8,∠A=30°,∠C=105°,求AB和BC的长.