题目内容
11.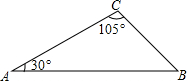 如图,已知AC=8,∠A=30°,∠C=105°,求AB和BC的长.
如图,已知AC=8,∠A=30°,∠C=105°,求AB和BC的长.
分析 过点C作CD⊥AB于D,根据直角三角形30°角所对的直角边等于斜边的一半求出CD,再根据∠C=105°,求出∠ACD和∠BCD的度数,根据勾股定理求出AD,再根据∠CDB=90°,求出∠CBD=∠BCD=45°,从而求出BD的值,最后根据AB=AD+DB,求出AB,再根据勾股定理求出BC即可.
解答 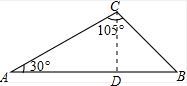 解:过点C作CD⊥AB于D,
解:过点C作CD⊥AB于D,
∵∠B=30°,AC=8,
∴CD=$\frac{1}{2}$AC=4,
∵∠C=105°,
∴∠ACD=90°-30°=60°,∠BCD=45°,
由勾股定理得,AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$,
∵∠CDB=90°,
∴∠CBD=∠BCD=45°,
∴CD=BD=4,
∴AB=AD+DB=4$\sqrt{3}$+4,
BC=$\sqrt{B{D}^{2}+C{D}^{2}}$=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$.
点评 本题考查了解直角三角形,用到的知识点是勾股定理,直角三角形30°角所对的直角边等于斜边的一半的性质,等腰直角三角形的判定与性质,熟记性质并作辅助线构造出两个特殊直角三角形是解题的关键.

练习册系列答案
相关题目
6.下面各式运用等式的性质变形,错误的是( )
| A. | 若x-3=y-3,则x=y | B. | 若$\frac{x}{a}$=$\frac{y}{a}$,则x=y | ||
| C. | 若a(c2+1)=b(c2+1),则a=b | D. | 若ac=bc,则a=b |
16.从-3,-1,1,5,6五个数中任取两个数相乘,若所得积中的最大值为a,最小值为b,则$\frac{a}{b}$的值为( )
| A. | -$\frac{5}{3}$ | B. | -2 | C. | -$\frac{5}{6}$ | D. | -10 |
20. 有理数a、b在数轴上对应的位置如图所示,其中正确的结论是( )
有理数a、b在数轴上对应的位置如图所示,其中正确的结论是( )
 有理数a、b在数轴上对应的位置如图所示,其中正确的结论是( )
有理数a、b在数轴上对应的位置如图所示,其中正确的结论是( )| A. | a+b>0 | B. | |a|>|b|>0 | C. | ab<0 | D. | a2>b2 |
 如图,四边形ABCD,M、N分别为AB、CD的中点,P、Q是连线的交点.求证:S四边形MQNP=S△APD+S△BQC.
如图,四边形ABCD,M、N分别为AB、CD的中点,P、Q是连线的交点.求证:S四边形MQNP=S△APD+S△BQC. 如图,抛物线y=ax2+2x+c经过点A(0,3),B(-1,0),请解答下列问题.
如图,抛物线y=ax2+2x+c经过点A(0,3),B(-1,0),请解答下列问题.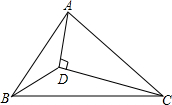 如图,在△ABC中,点D为△ABC内一点,连接AD,BD,CD,∠DBC=∠ACD=30°,∠ADC=90°,DB=3,BC=8,则AB的长为$\frac{10}{3}\sqrt{3}$.
如图,在△ABC中,点D为△ABC内一点,连接AD,BD,CD,∠DBC=∠ACD=30°,∠ADC=90°,DB=3,BC=8,则AB的长为$\frac{10}{3}\sqrt{3}$.