题目内容
△ABC是等边三角形,点A与点D的坐标分别是A(4,0),D(10,0).
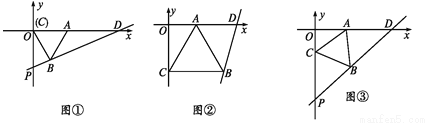
(1)如图①,当点C与点O重合时,求直线BD的表达式;
(2)如图②,点C从点O沿y轴向下移动,当以点B为圆心,AB为半径的☉B与y轴相切(切点为C)时,求点B的坐标;
(3)如图③,点C从点O沿y轴向下移动,当点C的坐标为C(0,-2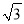 )时,求∠ODB的正切值.
)时,求∠ODB的正切值.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
△ABC是等边三角形,点A与点D的坐标分别是A(4,0),D(10,0).
(1)如图①,当点C与点O重合时,求直线BD的表达式;
(2)如图②,点C从点O沿y轴向下移动,当以点B为圆心,AB为半径的☉B与y轴相切(切点为C)时,求点B的坐标;
(3)如图③,点C从点O沿y轴向下移动,当点C的坐标为C(0,-2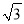 )时,求∠ODB的正切值.
)时,求∠ODB的正切值.

 阅读快车系列答案
阅读快车系列答案