题目内容
17. 如图数轴的A、B、C三点所表示的数分别为a、b、c.若|a-b|=3,|b-c|=5,且原点O与A、B的距离分别为4、1,则关于O的位置,下列叙述何者正确?( )
如图数轴的A、B、C三点所表示的数分别为a、b、c.若|a-b|=3,|b-c|=5,且原点O与A、B的距离分别为4、1,则关于O的位置,下列叙述何者正确?( )| A. | 在A的左边 | B. | 介于A、B之间 | C. | 介于B、C之间 | D. | 在C的右边 |
分析 由A、B、C三点表示的数之间的关系结合三点在数轴上的位置即可得出b=a+3,c=b+5,再根据原点O与A、B的距离分别为4、1,即可得出a=±4、b=±1,结合a、b、c间的关系即可求出a、b、c的值,由此即可得出结论.
解答 解:∵|a-b|=3,|b-c|=5,
∴b=a+3,c=b+5,
∵原点O与A、B的距离分别为4、1,
∴a=±4,b=±1,
∵b=a+3,
∴a=-4,b=-1,
∵c=b+5,
∴c=4.
∴点O介于B、C点之间.
故选C.
点评 本题考查了数值以及绝对值,解题的关键是确定a、b、c的值.本题属于基础题,难度不大,解决该题型题目时,根据数轴上点的位置关系分别找出各点代表的数是关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
7.某班10名学生的校服尺寸与对应人数如表所示:
则这10名学生校服尺寸的众数和中位数分别为( )
| 尺寸(cm) | 160 | 165 | 170 | 175 | 180 |
| 学生人数(人) | 1 | 3 | 2 | 2 | 2 |
| A. | 165cm,165cm | B. | 165cm,170cm | C. | 170cm,165cm | D. | 170cm,170cm |
8. 图中三视图对应的正三棱柱是( )
图中三视图对应的正三棱柱是( )
 图中三视图对应的正三棱柱是( )
图中三视图对应的正三棱柱是( )| A. |  | B. |  | C. |  | D. |  |
5.坐标平面上,某个一次函数的图形通过(5,0)、(10,-10)两点,判断此函数的图形会通过下列哪一点?( )
| A. | ($\frac{1}{7}$,9$\frac{4}{7}$) | B. | ($\frac{1}{8}$,9$\frac{5}{8}$) | C. | ($\frac{1}{9}$,9$\frac{7}{9}$) | D. | ($\frac{1}{10}$,9$\frac{9}{10}$) |
12.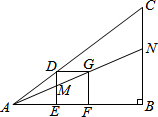 如图的△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直线AG分别交DE、BC于M、N两点.若∠B=90°,AB=4,BC=3,EF=1,则BN的长度为何?( )
如图的△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直线AG分别交DE、BC于M、N两点.若∠B=90°,AB=4,BC=3,EF=1,则BN的长度为何?( )
 如图的△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直线AG分别交DE、BC于M、N两点.若∠B=90°,AB=4,BC=3,EF=1,则BN的长度为何?( )
如图的△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直线AG分别交DE、BC于M、N两点.若∠B=90°,AB=4,BC=3,EF=1,则BN的长度为何?( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{8}{5}$ | D. | $\frac{12}{7}$ |
2.坐标平面上有一个二元一次方程式的图形,此图形通过(-3,0)、(0,-5)两点.判断此图形与下列哪一个方程式的图形的交点在第三象限?( )
| A. | x-4=0 | B. | x+4=0 | C. | y-4=0 | D. | y+4=0 |
 如图,在△ABC和△CED中,AB∥CD,AB=CE,AC=CD.求证:∠B=∠E.
如图,在△ABC和△CED中,AB∥CD,AB=CE,AC=CD.求证:∠B=∠E.