题目内容
9.坐标平面上,某二次函数图形的顶点为(2,-1),此函数图形与x轴相交于P、Q两点,且PQ=6.若此函数图形通过(1,a)、(3,b)、(-1,c)、(-3,d)四点,则a、b、c、d之值何者为正?( )| A. | a | B. | b | C. | c | D. | d |
分析 根据抛物线顶点及对称轴可得抛物线与x轴的交点,从而根据交点及顶点画出抛物线草图,根据图形易知a、b、c、d的大小.
解答 解:∵二次函数图形的顶点为(2,-1),
∴对称轴为x=2,
∵$\frac{1}{2}$×PQ=$\frac{1}{2}$×6=3,
∴图形与x轴的交点为(2-3,0)=(-1,0),和(2+3,0)=(5,0),
已知图形通过(2,-1)、(-1,0)、(5,0)三点,
如图,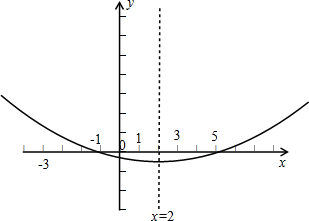
由图形可知:a=b<0,c=0,d>0.
故选:D.
点评 本题主要考查抛物线与x轴的交点,根据抛物线的对称性由对称轴及交点距离得出两交点坐标是解题的关键.

练习册系列答案
相关题目
19.-12等于( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
17. 如图数轴的A、B、C三点所表示的数分别为a、b、c.若|a-b|=3,|b-c|=5,且原点O与A、B的距离分别为4、1,则关于O的位置,下列叙述何者正确?( )
如图数轴的A、B、C三点所表示的数分别为a、b、c.若|a-b|=3,|b-c|=5,且原点O与A、B的距离分别为4、1,则关于O的位置,下列叙述何者正确?( )
 如图数轴的A、B、C三点所表示的数分别为a、b、c.若|a-b|=3,|b-c|=5,且原点O与A、B的距离分别为4、1,则关于O的位置,下列叙述何者正确?( )
如图数轴的A、B、C三点所表示的数分别为a、b、c.若|a-b|=3,|b-c|=5,且原点O与A、B的距离分别为4、1,则关于O的位置,下列叙述何者正确?( )| A. | 在A的左边 | B. | 介于A、B之间 | C. | 介于B、C之间 | D. | 在C的右边 |
4.若一正方形的面积为20平方公分,周长为x公分,则x的值介于下列哪两个整数之间?( )
| A. | 16,17 | B. | 17,18 | C. | 18,19 | D. | 19,20 |
14.计算(x2y)3的结果是( )
| A. | x6y3 | B. | x5y3 | C. | x5y | D. | x2y3 |
18. 如图,⊙O中,弦AB与CD交于点M,∠A=45°,∠AMD=75°,则∠B的度数是( )
如图,⊙O中,弦AB与CD交于点M,∠A=45°,∠AMD=75°,则∠B的度数是( )
 如图,⊙O中,弦AB与CD交于点M,∠A=45°,∠AMD=75°,则∠B的度数是( )
如图,⊙O中,弦AB与CD交于点M,∠A=45°,∠AMD=75°,则∠B的度数是( )| A. | 15° | B. | 25° | C. | 30° | D. | 75° |
