题目内容
如图,已知直线l1∥l2,线段AB在直线l1上,BC垂直于l1交l2于点C,且AB=BC,P是线段BC上异于两端点的一点,过点P的直线分别交l2、l1于点D、E(点A、E位于点B的两侧),满足BP=BE,连接AP、CE.
(1)求证:△ABP≌△CBE;
(2)连结AD、BD,BD与AP相交于点F.如图2.
①当
=2时,求证:AP⊥BD;
②当
=n(n>1)时,设△PAD的面积为S1,△PCE的面积为S2,求
的值.

(1)求证:△ABP≌△CBE;
(2)连结AD、BD,BD与AP相交于点F.如图2.
①当
| BC |
| BP |
②当
| BC |
| BP |
| S1 |
| S2 |

考点:相似形综合题
专题:几何综合题
分析:(1)求出∠ABP=∠CBE,根据SAS推出即可;
(2)①延长AP交CE于点H,求出AP⊥CE,证出△CPD∽△BPE,推出DP=PE,求出平行四边形BDCE,推出CE∥BD即可;
②分别用S表示出△PAD和△PCE的面积,代入求出即可.
(2)①延长AP交CE于点H,求出AP⊥CE,证出△CPD∽△BPE,推出DP=PE,求出平行四边形BDCE,推出CE∥BD即可;
②分别用S表示出△PAD和△PCE的面积,代入求出即可.
解答:(1)证明:∵BC⊥直线l1,
∴∠ABP=∠CBE,
在△ABP和△CBE中
∴△ABP≌△CBE(SAS);
(2)①证明:连结BD,延长AP交CE于点H,
∵△ABP≌△CBE,
∴∠APB=∠CEB,
∵∠PAB+∠APB=90°,
∴∠PAB+∠CEB=90°,
∴AH⊥CE,
∵
=2,即P为BC的中点,直线l1∥直线l2,
∴△CPD∽△BPE,
∴
=
=
,
∴DP=PE,
∴四边形BDCE是平行四边形,
∴CE∥BD,
∵AH⊥CE,
∴AP⊥BD;
②解:∵
=n,
∴BC=n•BP,
∴CP=(n-1)•BP,
∵CD∥BE,
易得△CPD∽△BPE,
∴
=
=n-1,
设△PBE的面积S△PBE=S,则△PCE的面积S△PCE满足
=
=n-1,
即S2=(n-1)S,
∵S△PAB=S△BCE=n•S,
∴S△PAE=(n+1)•S,
∵
=
=n-1,
∴S1=(n-1)•S△PAE,即S1=(n+1)(n-1)•S,
∴
=
=n+1.
∴∠ABP=∠CBE,
在△ABP和△CBE中
|
∴△ABP≌△CBE(SAS);
(2)①证明:连结BD,延长AP交CE于点H,

∵△ABP≌△CBE,
∴∠APB=∠CEB,
∵∠PAB+∠APB=90°,
∴∠PAB+∠CEB=90°,
∴AH⊥CE,
∵
| BC |
| BP |
∴△CPD∽△BPE,
∴
| DP |
| PE |
| CP |
| BP |
| 1 |
| 1 |
∴DP=PE,
∴四边形BDCE是平行四边形,
∴CE∥BD,
∵AH⊥CE,
∴AP⊥BD;
②解:∵
| BC |
| BP |
∴BC=n•BP,
∴CP=(n-1)•BP,
∵CD∥BE,
易得△CPD∽△BPE,
∴
| PD |
| PE |
| PC |
| PB |
设△PBE的面积S△PBE=S,则△PCE的面积S△PCE满足
| S△PCE |
| S△PBE |
| PC |
| PB |
即S2=(n-1)S,
∵S△PAB=S△BCE=n•S,
∴S△PAE=(n+1)•S,
∵
| S△PAD |
| S△PAE |
| PD |
| PE |
∴S1=(n-1)•S△PAE,即S1=(n+1)(n-1)•S,
∴
| S1 |
| S2 |
| (n+1)(n-1)S |
| (n-1)S |
点评:本题考查了平行四边形的性质和判定,相似三角形的性质和判定,全等三角形的性质和判定的应用,主要考查了学生的推理能力,题目比较好,有一定的难度.

练习册系列答案
相关题目
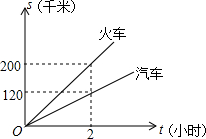 已知A、B两地的路程为240千米,某经销商每天都要用汽车或火车将x吨保鲜品一次性由A地运往B地,受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订,现有货运收费项目及收费标准表、行驶路程s(千米)与行驶时间t(时间)的函数图象,如图.
已知A、B两地的路程为240千米,某经销商每天都要用汽车或火车将x吨保鲜品一次性由A地运往B地,受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订,现有货运收费项目及收费标准表、行驶路程s(千米)与行驶时间t(时间)的函数图象,如图.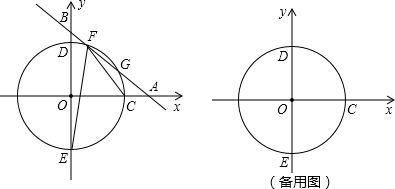

 在△ABC中,点E在AC上,且
在△ABC中,点E在AC上,且
 如图,△ABC中,D、E分别是AB、AC的中点,若△ADE的面积为2,则四边形DECB的面积是
如图,△ABC中,D、E分别是AB、AC的中点,若△ADE的面积为2,则四边形DECB的面积是