题目内容
某学习小组由3名男生和1名女生组成,在一次合作学习后,开始进行成果展示.
(1)如果随机抽取1名同学单独展示,那么女生展示的概率为 ;
(2)如果随机抽取2名同学共同展示,求同为男生的概率.
(1)如果随机抽取1名同学单独展示,那么女生展示的概率为
(2)如果随机抽取2名同学共同展示,求同为男生的概率.
考点:列表法与树状图法
专题:计算题
分析:(1)4名学生中女生1名,求出所求概率即可;
(2)列表得出所有等可能的情况数,找出同为男生的情况数,即可求出所求概率.
(2)列表得出所有等可能的情况数,找出同为男生的情况数,即可求出所求概率.
解答:解:(1)如果随机抽取1名同学单独展示,那么女生展示的概率为
;
(2)列表如下:
所有等可能的情况有12种,其中同为男生的情况有6种,
则P=
=
.
| 1 |
| 4 |
(2)列表如下:
| 男 | 男 | 男 | 女 | |
| 男 | --- | (男,男) | (男,男) | (女,男) |
| 男 | (男,男) | --- | (男,男) | (女,男) |
| 男 | (男,男) | (男,男) | --- | (女,男) |
| 女 | (男,女) | (男,女) | (男,女) | --- |
则P=
| 6 |
| 12 |
| 1 |
| 2 |
点评:此题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
抛物线y=(x-1)2+4的最小值是( )
| A、4 | B、1 | C、-1 | D、5 |
按如图所示的程序计算,若开始输入的n值为
,则最后输出的结果是( )
| 2 |

| A、14 | ||
| B、16 | ||
C、8+5
| ||
D、14+
|
 如图,AB,AC分别是半⊙O的直径和弦,OD⊥AC于点D,过点A作半⊙O的切线AP,AP与OD的延长线交于点P.连接PC并延长与AB的延长线交于点F.
如图,AB,AC分别是半⊙O的直径和弦,OD⊥AC于点D,过点A作半⊙O的切线AP,AP与OD的延长线交于点P.连接PC并延长与AB的延长线交于点F.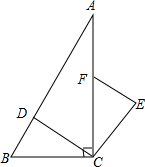 如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.
如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF. 一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)
一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6) 在矩形ABCD中,BC=8cm,对角线AC比AB多4cm,BE⊥AC于点E,求BE的长.
在矩形ABCD中,BC=8cm,对角线AC比AB多4cm,BE⊥AC于点E,求BE的长.