题目内容
在△ABC中，点E在AC上，且| AE |
| EC |
| 1 |
| 2 |
| BD |
| DC |
| 1 |
| 3 |
考点：平行线分线段成比例,三角形中位线定理
专题：证明题
分析：过点E作EG∥AD交BC于G，然后判断出DF是△BEG的中位线，从而求出BD=DG，再求出
，然后根据平行线分线段成比例定理证明即可．
| AE |
| AC |
解答：
证明：如图，过点E作EG∥AD交BC于G，
∵F为BE中点，
∴DF是△BEG的中位线，
∴BD=DG，
∵
=
，
∴
=
=
，
∵EG∥AD，
∴
=
=
，
∴
=
．
证明：如图，过点E作EG∥AD交BC于G，∵F为BE中点，
∴DF是△BEG的中位线，
∴BD=DG，
∵
| AE |
| EC |
| 1 |
| 2 |
∴
| AE |
| AC |
| 1 |
| 1+2 |
| 1 |
| 3 |
∵EG∥AD，
∴
| DG |
| DC |
| AE |
| AC |
| 1 |
| 3 |
∴
| BD |
| DC |
| 1 |
| 3 |
点评：本题考查了平行线分线段成比例定理，三角形的中位线定理，此类题目，过点E作出辅助线是解题的关键，也是本题的难点．
练习册系列答案
活力课时同步练习册系列答案
相关题目
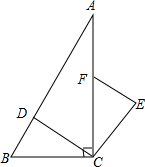如图，在Rt△ABC中，∠ACB=90°，点D、F分别在AB、AC上，CF=CB，连接CD，将线段CD绕点C按顺时针方向旋转90°后得CE，连接EF．
如图，抛物线y=-