题目内容
AB是⊙O的直径，P为AB延长线上一点，PC与圆O相切于点C，AD⊥PC于D，若PC=4，PB=2，求PD的长．考点：切线的性质
专题：计算题
分析：连接OC，如图，设⊙O的半径为r，根据切线的性质得OC⊥PC，在Rt△COP中，利用勾股定理得r2+42=（r+2）2，解得r=3，则PO=5，PA=8，由于AD⊥PD，
则OC∥AD，根据平行线分线段成比例定理得到
=
，然后根据比例性质计算PD的长．
则OC∥AD，根据平行线分线段成比例定理得到
| PC |
| PD |
| PO |
| PA |
解答：解：连接OC，如图，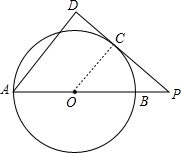
设⊙O的半径为r，
∵PC与圆O相切于点C，
∴OC⊥PC，
在Rt△COP中，OC=r，OP=OB+PB=r+2，PC=4，
∵OC2+PC2=OP2，
∴r2+42=（r+2）2，解得r=3，
∴PO=5，PA=8，
∵AD⊥PD，
∴OC∥AD，
∴
=
，即
=
，
∴PD=
．
设⊙O的半径为r，∵PC与圆O相切于点C，
∴OC⊥PC，
在Rt△COP中，OC=r，OP=OB+PB=r+2，PC=4，
∵OC2+PC2=OP2，
∴r2+42=（r+2）2，解得r=3，
∴PO=5，PA=8，
∵AD⊥PD，
∴OC∥AD，
∴
| PC |
| PD |
| PO |
| PA |
| 4 |
| PD |
| 5 |
| 8 |
∴PD=
| 32 |
| 5 |
点评：本题考查了切线的性质：圆的切线垂直于经过切点的半径．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．
练习册系列答案
相关题目
已知∠O及其边上两点A和B（如图），用直尺和圆规作一点P，使点P到∠O的两边的距离相等，且到点A、B的距离也相等．（保留作图痕迹）
已知三条平行的直线a、b、c，试作等边△ABC，使其顶点分别在a、b上，在直线a上取一点A，作AD⊥b，D为垂足．再作AD′=AD，∠DAD′=60°，过D′作D′C⊥AD′交直线c与点C，则AC为正三角形的边长，以AC为半径，A为圆心画弧，交直线b于点B，连接BC，则△ABC即为所求．你认为上述作法是否正确？为什么？请加以说明．