题目内容
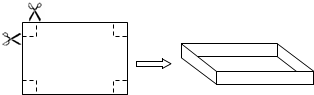
如图,把一张长10cm,宽8 cm的矩形硬纸板的四周各剪去一个同样大小的正方形,再折合成一个无盖的长方体盒子(纸板的厚度忽略不计),从美观的角度考虑要求底面的短边与长边的比不小于
,设四周小正方形的边长为x cm
(1)求盒子的侧面积S侧与x的函数关系式,并求x的取值范围;
(2)求当正方形的边长x为何值时侧面积S侧有最大值;
(3)若要求侧面积不小于28cm2,直接写出正方形的边长x的取值范围.
| 2 |
| 3 |
(1)求盒子的侧面积S侧与x的函数关系式,并求x的取值范围;
(2)求当正方形的边长x为何值时侧面积S侧有最大值;
(3)若要求侧面积不小于28cm2,直接写出正方形的边长x的取值范围.

考点:二次函数的应用
专题:
分析:(1)由长方体的侧面积=四个长方形的面积之和就可以表示出S侧与x之间关系式,由底面的短边与长边的比不小于
建立不等式就可以求出x的取值范围;
(2)由(1)的解析式根据二次函数的性质就可以求出最大值;
(3)由侧面积不小于28cm2,建立不等式求出其解即可.
| 2 |
| 3 |
(2)由(1)的解析式根据二次函数的性质就可以求出最大值;
(3)由侧面积不小于28cm2,建立不等式求出其解即可.
解答:解:(1)由题意,得
S侧=2(10-2x)x+2(8-2x)x,
S侧=-8x2+36x.
∵
≥
,
∴x≤2.
∵x>0,
∴0<x≤2;
(2)∵S侧=-8x2+36x.
∴S侧=-8x2+36x.
∴S侧=-8(x-
)2+
.
∴a=-8<0
∴x=
时,S侧最大=
,
∴在对称轴的左侧,S侧随x的增而增大,
∵0<x≤2;
∴当x=2时,S侧=40
答:当x=2时,S侧有最大值为40;
(3)由题意,得
-8x2+36x≥28,
2x2-9x+7≤0,
(x-1)(2x-7)≤0,
∴①
,②
,
解①,得原不等式组无解,
解②,得1≤x≤
.
故正方形的边长x的取值范围是:1≤x≤
.
S侧=2(10-2x)x+2(8-2x)x,
S侧=-8x2+36x.
∵
| 8-2x |
| 10-2x |
| 2 |
| 3 |
∴x≤2.
∵x>0,
∴0<x≤2;
(2)∵S侧=-8x2+36x.
∴S侧=-8x2+36x.
∴S侧=-8(x-
| 9 |
| 4 |
| 81 |
| 2 |
∴a=-8<0
∴x=
| 9 |
| 4 |
| 81 |
| 2 |
∴在对称轴的左侧,S侧随x的增而增大,
∵0<x≤2;
∴当x=2时,S侧=40
答:当x=2时,S侧有最大值为40;
(3)由题意,得
-8x2+36x≥28,
2x2-9x+7≤0,
(x-1)(2x-7)≤0,
∴①
|
|
解①,得原不等式组无解,
解②,得1≤x≤
| 7 |
| 2 |
故正方形的边长x的取值范围是:1≤x≤
| 7 |
| 2 |
点评:本题考查了长方体的侧面积的运用,二次函数的性质的运用,自变量的取值范围的运用,一元二次不等式的运用,解答时求出二次函数的解答式是关键.

练习册系列答案
相关题目
 如图,△ABC≌△DBE,AB与DB,AC与DE是对应边,已知:∠B=43°,∠A=30°,求∠BED的度数.请你完善下面的推理步骤:解:∵∠A+∠B+∠BCA=180°(
如图,△ABC≌△DBE,AB与DB,AC与DE是对应边,已知:∠B=43°,∠A=30°,求∠BED的度数.请你完善下面的推理步骤:解:∵∠A+∠B+∠BCA=180°( AB是⊙O的直径,P为AB延长线上一点,PC与圆O相切于点C,AD⊥PC于D,若PC=4,PB=2,求PD的长.
AB是⊙O的直径,P为AB延长线上一点,PC与圆O相切于点C,AD⊥PC于D,若PC=4,PB=2,求PD的长. 如图,将矩形ABCD纸片沿对角线BD折叠,使点C落在C′处,C′D交AB于E,若∠BDC′=22.5°则在不添加任何辅助线的情况下,图中45°的角(图中虚线也可视为角的边)有( )
如图,将矩形ABCD纸片沿对角线BD折叠,使点C落在C′处,C′D交AB于E,若∠BDC′=22.5°则在不添加任何辅助线的情况下,图中45°的角(图中虚线也可视为角的边)有( )