题目内容
1.如果关于x的分式方程$\frac{a}{x+1}$-3=$\frac{1-x}{x+1}$有负分数解,且关于x的不等式组$\left\{\begin{array}{l}{2(a-x)≥-x-4}\\{\frac{3x+4}{2}<x+1}\end{array}\right.$的解集为x<-2,那么符合条件的所有整数a的积是( )| A. | -3 | B. | 0 | C. | 3 | D. | 9 |
分析 把a看做已知数表示出不等式组的解,根据已知解集确定出a的范围,分式方程去分母转化为整式方程,将a的整数解代入整式方程,检验分式方程解为负分数确定出所有a的值,即可求出之积.
解答 解:$\left\{\begin{array}{l}{2(a-x)≥-x-4①}\\{\frac{3x+4}{2}<x+1②}\end{array}\right.$,
由①得:x≤2a+4,
由②得:x<-2,
由不等式组的解集为x<-2,得到2a+4≥-2,即a≥-3,
分式方程去分母得:a-3x-3=1-x,
把a=-3代入整式方程得:-3x-6=1-x,即x=-$\frac{7}{2}$,符合题意;
把a=-2代入整式方程得:-3x-5=1-x,即x=-3,不合题意;
把a=-1代入整式方程得:-3x-4=1-x,即x=-$\frac{5}{2}$,符合题意;
把a=0代入整式方程得:-3x-3=1-x,即x=-2,不合题意;
把a=1代入整式方程得:-3x-2=1-x,即x=-$\frac{3}{2}$,符合题意;
把a=2代入整式方程得:-3x-1=1-x,即x=-1,不合题意;
把a=3代入整式方程得:-3x=1-x,即x=-$\frac{1}{2}$,符合题意;
∴符合条件的整数a取值为-3,-1,1,3,之积为9,
故选D
点评 此题考查了解一元一次不等式组,以及解分式方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
12.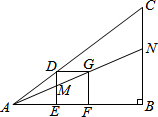 如图的△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直线AG分别交DE、BC于M、N两点.若∠B=90°,AB=4,BC=3,EF=1,则BN的长度为何?( )
如图的△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直线AG分别交DE、BC于M、N两点.若∠B=90°,AB=4,BC=3,EF=1,则BN的长度为何?( )
 如图的△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直线AG分别交DE、BC于M、N两点.若∠B=90°,AB=4,BC=3,EF=1,则BN的长度为何?( )
如图的△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直线AG分别交DE、BC于M、N两点.若∠B=90°,AB=4,BC=3,EF=1,则BN的长度为何?( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{8}{5}$ | D. | $\frac{12}{7}$ |
9.坐标平面上,某二次函数图形的顶点为(2,-1),此函数图形与x轴相交于P、Q两点,且PQ=6.若此函数图形通过(1,a)、(3,b)、(-1,c)、(-3,d)四点,则a、b、c、d之值何者为正?( )
| A. | a | B. | b | C. | c | D. | d |
16.若二次根式$\sqrt{a-2}$有意义,则a的取值范围是( )
| A. | a≥2 | B. | a≤2 | C. | a>2 | D. | a≠2 |
13.已知x-2y=3,那么代数式3-2x+4y的值是( )
| A. | -3 | B. | 0 | C. | 6 | D. | 9 |
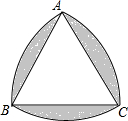 如图,△ABC是等边三角形,AB=2,分别以A,B,C为圆心,以2为半径作弧,则图中阴影部分的面积是2π-3$\sqrt{3}$.
如图,△ABC是等边三角形,AB=2,分别以A,B,C为圆心,以2为半径作弧,则图中阴影部分的面积是2π-3$\sqrt{3}$. 如图,在△ABC和△CED中,AB∥CD,AB=CE,AC=CD.求证:∠B=∠E.
如图,在△ABC和△CED中,AB∥CD,AB=CE,AC=CD.求证:∠B=∠E. 如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$的图象的两个交点.
如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$的图象的两个交点.