题目内容
7.在?ABCD中,对角线AC与BD交于点O,且AO=BO,若∠AOB=60°,AB=2,则?ABCD的面积是4$\sqrt{3}$.分析 首先证明四边形ABCD是矩形,利勾股定理求出AD即可解决问题.
解答 解:如图,∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵OA=OB,
∴BD=AC,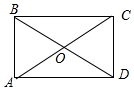
∴四边形ABCD是矩形,
∵OA=OB,∠AOB=60°,
∴△AOB是等边三角形,
∴OB=OD=2,
在Rt△ABD中,AD=$\sqrt{B{D}^{2}-A{B}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴矩形ABCD的面积=AB•AD=2×2$\sqrt{3}$=4$\sqrt{3}$.
故答案为4$\sqrt{3}$.
点评 本题考查平行四边形的性质,矩形的判定和性质、勾股定理等知识,解题的关键是发现四边形ABCD是矩形,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

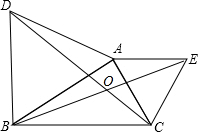 △ABD和△AEC都是等边三角形,连CD、BE,若BE=6,求DC的长.
△ABD和△AEC都是等边三角形,连CD、BE,若BE=6,求DC的长.