题目内容
5.已知:A=4x2-4xy+y2,B=x2+xy-5y2.求:(1)3A-2B=?
(2)2A+B=?
(3)(3A-2B)-(2A+B)的值.
分析 (1)把A与B代入3A-2B,去括号合并即可得到结果;
(2)把A与B代入2A+B中,去括号合并即可得到结果;
(3)原式去括号合并后,将A与B代入计算即可求出值.
解答 解:(1)3A-2B=3(4x2-4xy+y2)-2(x2+xy-5y2)=10 x2-14 xy+13 y2;
(2)2A+B=2(4x2-4xy+y2)+x2+xy-5y2=9x2-7xy-3y2;
(3)(3A-2B)-(2A+B)=3A-2B-2A-B=A-3B=x2-7xy+16y2.
点评 此题考查了整式的加减-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
16.如图,直角三角形纸片ABC中AB=3,AC=4,D为斜边BC中点,第1次将纸片折叠,使点A与点D重合,折痕与AD交于点P1;设P1D的中点为D1,第2次将纸片折叠,使点A与点D1重合,折痕与AD交于P2;设P2D1的中点为D2,第3次将纸片折叠,使点A与点D2重合,折痕与AD交于点P3;设Pn-1Dn-2的中点为Dn-1,第n次将纸片折叠,使点A与点Dn-1重合,折痕与AD交于点Pn(n>2),则AP6的长为( )


| A. | $\frac{{3}^{5}}{5×{2}^{9}}$ | B. | $\frac{5×{3}^{5}}{{2}^{12}}$ | C. | $\frac{5×{3}^{6}}{{2}^{14}}$ | D. | $\frac{{3}^{7}}{5×{2}^{11}}$ |
13. 如图,一边靠校园围墙,其他三边用总长为80米的铁栏杆围成一个矩形花圃,设矩形ABCD的边AB为x米,面积为S平方米,要使矩形ABCD面积最大,则x的长为( )
如图,一边靠校园围墙,其他三边用总长为80米的铁栏杆围成一个矩形花圃,设矩形ABCD的边AB为x米,面积为S平方米,要使矩形ABCD面积最大,则x的长为( )
 如图,一边靠校园围墙,其他三边用总长为80米的铁栏杆围成一个矩形花圃,设矩形ABCD的边AB为x米,面积为S平方米,要使矩形ABCD面积最大,则x的长为( )
如图,一边靠校园围墙,其他三边用总长为80米的铁栏杆围成一个矩形花圃,设矩形ABCD的边AB为x米,面积为S平方米,要使矩形ABCD面积最大,则x的长为( )| A. | 40米 | B. | 30米 | C. | 20米 | D. | 10米 |
10.若向东走15米记为+15米,则向西走28米记为( )
| A. | -28米 | B. | +28米 | C. | 56米 | D. | -56米 |
20.一小商店一周的盈亏情况如表(亏为负),单位:元
(1)计算出小商店一周的盈亏情况;
(2)指出盈利最多一天的盈利额.
| 星期 | 周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
| 盈亏情况 | 128.3 | -25.6 | -15 | 27 | -7 | 36.5 | 98 |
(2)指出盈利最多一天的盈利额.
 如图,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为2的顶点上时,那么他应走2个边长,即从2→3→4为第一次“移位”,这时他到达编号为4的顶点;然后从4→3为第二次“移位”.若小宇从编号为3的顶点开始,第2017次“移位”后,则他所处顶点的编号是1.
如图,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为2的顶点上时,那么他应走2个边长,即从2→3→4为第一次“移位”,这时他到达编号为4的顶点;然后从4→3为第二次“移位”.若小宇从编号为3的顶点开始,第2017次“移位”后,则他所处顶点的编号是1. 如图,AB=AC,若使△ABE≌△ACF,则还需要添加的条件是∠B=∠C.(只要写出一个答案).
如图,AB=AC,若使△ABE≌△ACF,则还需要添加的条件是∠B=∠C.(只要写出一个答案).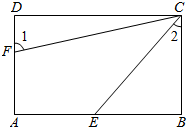 如图,已知四边形ABCD是平行四边形,并且∠A=∠D.
如图,已知四边形ABCD是平行四边形,并且∠A=∠D.