题目内容
5．
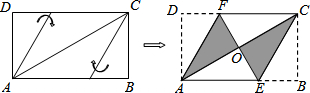将矩形纸片ABCD按如图所示的方式折叠，得到菱形AECF．若AB=3，则BC的长为 （ ）| A． | 2 | B． | 1 | C． | $\sqrt{2}$ | D． | $\sqrt{3}$ |
分析 根据菱形及矩形的性质可得到∠BAC的度数，从而根据直角三角形的性质求得BC的长．
解答 解：∵AECF为菱形，
∴∠FCO=∠ECO，
由折叠的性质可知，∠ECO=∠BCE，
又∠FCO+∠ECO+∠BCE=90°，
∴∠FCO=∠ECO=∠BCE=30°，
在Rt△EBC中，EC=2EB，
又EC=AE，
AB=AE+EB=3，
∴EB=1，EC=2，
∴Rt△BCE中，BC=$\sqrt{3}$，
故选：D．
点评 本题主要考查了菱形的性质以及矩形的性质，解决问题的关键是根据折叠以及菱形的性质发现特殊角，根据30°的直角三角形中各边之间的关系求得BC的长．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
如图，四边形ABCD中，AB∥CD，∠DAB=90°，且∠ABC=60°，AB=BC，△ABC的外接圆⊙O交BC于E点，连接DE并延长，交AB的延长线于F，求证：CF=DB．
20．估算$\sqrt{17}$+1的值在（ ）
| A． | 5和6之间 | B． | 3和4之间 | C． | 4和5之间 | D． | 2和3之间 |
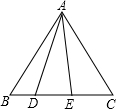在等边三角形ABC中，点D在BC上，且BD：DC=1：4，连接DA，作∠DAE，满足∠DAE=30°，则tan∠BAE的值是$\frac{\sqrt{3}}{2}$．