题目内容
13.计算:(1)99×101
(2)992.
分析 (1)根据平方差公式,可得答案;(2)根据完全平方公式,可得答案.
解答 解:(1)99×101=(100-1)(100+1)=1002-1=9999;
(2)992=(100-1)2=1002-2×100+1=9801.
点评 本题考查了平方差公式,利用公式是解题关键.

练习册系列答案
相关题目
3.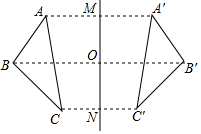 如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法不一定正确的是( )
如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法不一定正确的是( )
 如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法不一定正确的是( )
如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法不一定正确的是( )| A. | AC=A′C′ | B. | BO=B′O | C. | AA′⊥MN | D. | AB∥B′C′ |
4.某射击运动员进行两次射击(每次射击成绩最小环数是0环,最大环数是10环),则下列说法中正确的是( )
| A. | “该运动员两次的射击成绩都是9环”属于随机事件 | |
| B. | “该运动员一次的射击成绩为10环,一次的射击成绩为0环”属于不可能事件 | |
| C. | “该运动员两次的射击成绩的总成绩为21环”属于必然事件 | |
| D. | 该运动员一次的射击成绩大于6环的可能性比大于8环的可能性小 |
5.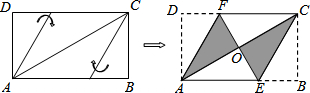 将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为 ( )
将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为 ( )
 将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为 ( )
将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为 ( )| A. | 2 | B. | 1 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
3.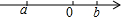 在数轴上实数a,b的位置如图所示,化简|a+b|+$\sqrt{(a-b)^{2}}$的结果是( )
在数轴上实数a,b的位置如图所示,化简|a+b|+$\sqrt{(a-b)^{2}}$的结果是( )
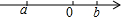 在数轴上实数a,b的位置如图所示,化简|a+b|+$\sqrt{(a-b)^{2}}$的结果是( )
在数轴上实数a,b的位置如图所示,化简|a+b|+$\sqrt{(a-b)^{2}}$的结果是( )| A. | -2a-b | B. | -2a+b | C. | -2b | D. | -2a |
 如图,在直角坐标系中,直线l与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1,以A1B、BA为邻边作?ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1、B1A1为邻边作?A1B1A2C2;…;按此作法继续下去,则C3的坐标是(-16$\sqrt{3}$,64);Cn的坐标是(-22(n-1)$\sqrt{3}$,22n)(n为正整数).
如图,在直角坐标系中,直线l与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1,以A1B、BA为邻边作?ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1、B1A1为邻边作?A1B1A2C2;…;按此作法继续下去,则C3的坐标是(-16$\sqrt{3}$,64);Cn的坐标是(-22(n-1)$\sqrt{3}$,22n)(n为正整数). 一个正方体的平面展开图,如图所示,将它折成正方体后“水”字对面是设.
一个正方体的平面展开图,如图所示,将它折成正方体后“水”字对面是设.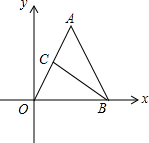 如图,在直角坐标系中有一个等腰△AOB,点O为坐标原点,AO=AB,OB=4,tan∠AOB=2,点C是线段OA的中点.
如图,在直角坐标系中有一个等腰△AOB,点O为坐标原点,AO=AB,OB=4,tan∠AOB=2,点C是线段OA的中点.