题目内容
2.计算:($\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2006}$)(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2005}$)-(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2006}$)($\frac{1}{2}$+$\frac{1}{3}$+…$\frac{1}{2005}$).分析 不妨设a=$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2006}$,b=$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2005}$,把原式化简,进一步计算即可.
解答 解:设a=$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2006}$,b=$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2005}$,
原式=a(1+b)-(1+a)b
=a+ab-b-ab
=a-b
=$\frac{1}{2006}$.
点评 此题考查整式的混合运算,注意整体思想的渗透.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
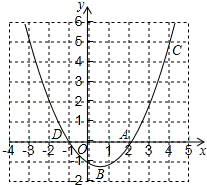 如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三点.
如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三点.